Problem S. 46. (September 2009)

S. 46. Unlike most belief systems, Flagland's mythology is deeply interlaced with elements of natural sciences. They think for example that it brings misfortune if the main sail of a ship is not square-shaped, or its side length (in meters) is not a power of 2. According to this, only square-shaped sailcloths with side length of a power of 2 are sold in local harbors, and tailors only join up 4 sailcloths of the same size to produce a twice as big sail.

Create your program to calculate the minimal price of a sailcloth of required size, if prices of various available sailcloths are known.

The first line of the standard input contains three integers (separated by a space): the number of available sailcloths on the market, the side length 1A=2^a2048 of the required sailcloth, and the sewing cost 0V1000 in (linear) meters. Then each of the following N lines contains two integers: the side lengths 1B_i=2^b_iA of available sailcloths and their prices . Lines of the input are ordered monotonically first according to side lengths, then to prices.

The only line of the standard output should contain a single integer: the minimal price to make the required sailcloth. (This price consists of the cost of materials and possible sewing.) You can assume that a solution always exists.

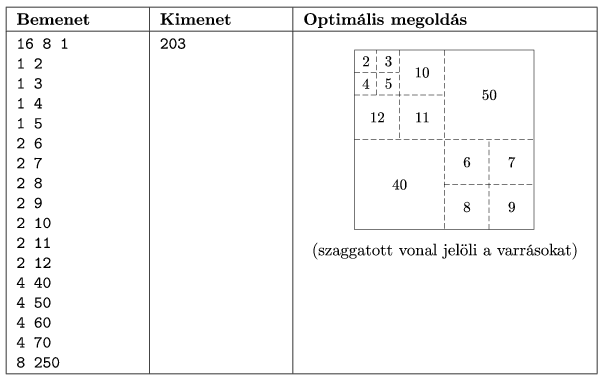
In the figure, ``Bemenet'' is input, ``Kimenet'' is output, ``Optimális megoldás'' is the optimal solution, while ``szaggatott vonal jelöli a varrásokat'' is ``seams are denoted by dashed lines''.

The source code and project files of your solution (without the .exe file or any other auxiliary files generated by the compiler) together with a short documentation describing your solution should be submitted in a compressed folder (s46.zip).

Sample test cases: s46teszt.zip. Your solution has to give (a not neccessarily correct) answer to 5 out of 10 inputs in order to be judged.

(10 pont)

Deadline expired on October 12, 2009.

Statistics:

27 students sent a solution.
10 points:	Berecz Dénes, Éles András, Mokcsay 026 Ádám, Várnai Péter.
9 points:	Adrián Patrik, Bodosi Eszter, Fejér 267 László, Kovács 125 András, Nagy 111 Miklós, Nagy Róbert.
8 points:	8 students.
7 points:	4 students.
6 points:	2 students.
5 points:	1 student.
4 points:	1 student.
3 points:	1 student.

Problems in Information Technology of KöMaL, September 2009