 Problem S. 56. (October 2010)
Problem S. 56. (October 2010)
S. 56. You are given the road map of a town with junctions and the two-way streets connecting them. You would like to travel all junctions (but all streets do not have to be travelled) with a bus that can not go reverse, so it can not return to the junction immediately visited. (Otherwise all streets and junctions can be visited arbitrarily.)
Your program should read the road map of the town from the standard input, then determine a sequence of junctions that contain all of them, consecutive junctions are directly connected, but there is no ,,direct return'' (in the sense that there are no 3 consecutive junctions in the sequence with the first and third being the same). We can assume that any two junctions are connected by at most one street, the road map is connected (that is, one can travel from any junction to any other), further, there is no dead end in the town (that is, a junction connected to only one street).
The first line of the input contains 2 integers separated by a space, the number of junctions in the town and the number of streets
. Then each of the following M lines contains the two endpoints Xi, Yi of a street (separated by a space) with 1
 Xi
Xi Yi
Yi N.
N.
The only line of the standard output should be the sequence of junctions satisfying the above criteria.
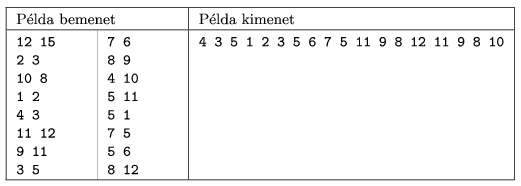
We have given a sample input (Példa bemenet) and a possible output (Példa kimenet).
The source code and project files of your solution -- without the .exe or any other auxiliary files generated by the compiler -- should be submitted together with a short documentation (s56.txt, s56.pdf, ...) in a compressed folder s56.zip.
(10 pont)
Deadline expired on November 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
A feladatot háromféleképpen is meg lehetett oldani.
1. A legegyszerűbb megoldás a következő: Elindulunk az első csúcsból, folyamatosan számon tartjuk, hogy melyik csúcsban hányszor jártunk, és az aktuális csúcsnak mindig abba a szomszédjába lépünk, amelyikben eddig a legkevesebbszer voltunk (a szomszédok közül nem vesszük figyelembe a megfordulási feltétel által kizárt csúcsot). Az algoritmus akkor ér véget, ha már bejártunk minden csúcsot (ennek ellenőrzéséhez számon tartjuk, hogy hány csúcsban jártunk már). Erről nem könnyű belátni, hogy mindig eredményt ad, azaz hogy nem kerülhet esetleg végtelen ciklusba. A bizonyítás és a forráskód: egyszeru.zip. A beküldött megoldások között nem volt 100 sor alatti, viszont ez a megoldás kevesebb, mint 50 sorban megírható.
2. A mélységi bejárást használó megoldást Borsos Zalán 12. osztályos marosvásárhelyi versenyzőnek sikerült tökéletesre megcsinálnia. DFS.zip
3. A széltében kereséses megoldás senkinek sem sikerült tökéletesre. Többféle elvi, illetve implementálási hiba előjött. Adrián Patrik 11. osztályos debreceni tanulónak csak az implementációban volt hiba, úgyhogy az ő megoldásának javított változatát adjuk közre. BFS.zip Volt olyan, aki az egész széltében keresésből kizárta a legutóbb meglátogatott csúcsot (ahelyett, hogy csak a kiinduló csúcs szomszédai közül zárta volna ki). Ez hibát okoz pl. ebben a tesztesetben, be1.txt amikor az 1, 2, 3 csúcsok bejárása után a 4-es csúcsba kéne eljutni. Olyan is volt, aki mindig előre kijelölte, hogy melyik csúcsba szeretne menni. Ez azért okoz hibát, mert nem biztosított, hogy minden széltében keresésnél el tudunk jutni az összes csúcsba.
Maximális méretű bemenetekre a futási idők az alábbiak körül alakultak (tized mp-ben):
Ritka gráfokra (kb. 60000 él): 1. megoldás: 5, 2. megoldás: 50, 3. megoldás: 4
Sűrűbb gráfokra (kb. 500000 él): 1. megoldás: 25, 2. megoldás: 16, 3. megoldás: 50
A leghosszabb sétákat általában a mélységi bejárásos megoldás adta (10000 csúcsú, ritka gráfokra több százszor hosszabbakat, mint a másik két megoldás). Az 1. megoldás által adott út hossza minden tesztesetnél belül volt a gráf csúcsszámának 2.125-szörösén.
Voltak, akik backtrack-el próbálkoztak de ezek a megoldások túl lassúak voltak nagyobb tesztesetekre.
Statistics:
9 students sent a solution. 10 points: Borsos 607 Zalán. 9 points: Nagy 111 Miklós, Szabó 928 Attila. 7 points: 3 students. 6 points: 1 student. 4 points: 1 student. 3 points: 1 student.
Problems in Information Technology of KöMaL, October 2010
