 Problem S. 57. (November 2010)
Problem S. 57. (November 2010)
S. 57. We would like to cover a chessboard with dominoes (without gaps or any overlapping) in such a way that some squares of the board are previously excluded (so that no domino can be put on those squares).
Your program should read the size of the board and the excluded squares from the standard input, then compute a suitable cover, if it exists.
The structure of the input is the following: the first line contains two integers separated with a space, denoting the size of the board (\(\displaystyle 1\le N \le 100\)) and the number of excluded squares (\(\displaystyle 0 \le M \le N\cdot N\)). Then each of the following \(\displaystyle M\) lines contains the row and column coordinates of the excluded squares (again, separated with a space).
If there exists a suitable cover, then your program should write \(\displaystyle N\) lines to the standard output, with each line having \(\displaystyle N\) numbers. The number in the \(\displaystyle i^{\rm th}\) row and \(\displaystyle j^{\rm th}\) column gives the number of the domino covering the \(\displaystyle i^{\rm th}\) row and \(\displaystyle j^{\rm th}\) column of the chessboard, if that square is not excluded, otherwise that number should be 0. Numbering of the dominoes is arbitrary (different dominoes however should have different numbers). If there is no solution, you should display the message ``this board can not be covered''. The time limit for your program in each test case will be at most 10 seconds.
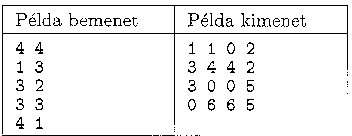
In the example, ``Példa bemenet'' is the sample input, while ``Példa kimenet'' is the corresponding output.
The source code and project files of your solution -- without the .exe or any other auxiliary files generated by the compiler -- should be submitted together with a short documentation in a compressed folder s57.zip. One can obtain 8 points if the program can solve any test cases of the above type within 10 seconds. (If the running time exceeds 10 seconds, we will consider that test case unsolved.) 5 points can be awarded if your program can cover boards of size at most 10 by 10. Further 2 points can be obtained for documentation.
(10 pont)
Deadline expired on December 10, 2010.
Sorry, the solution is available only in Hungarian. Google translation
A bemenetet felfoghatjuk egy gráfnak, ahol a csúcsok a sakktábla nem kizárt mezői, és a szomszédos mezőknek megfelelő csúcsok vannak éllel összekötve. Jól látható, hogy páros gráfot kaptunk, hiszen csak ellentétes színű mezőket kötöttünk össze. Egy dominó megfelel a gráf egy élének, egy dominóhalmaz pedig megfelel egy párosításnak a gráfban, mert az a feltétel, hogy nem lehet a párosításban két olyan él, aminek van közös pontja, megfelel annak a feltételnek, hogy nem fedhetnek át a dominók. Egy hézagmentes lefedés megfelel egy teljes párosításnak. Teljes párosítást kereshetünk pl. a Magyar Módszer nevű algoritmussal. Ennek a megoldásnak a bemutatására Nagy Róbert 10. osztályos budapesti tanuló megoldását tesszük közzé.
Többen backtrack-kel próbálták megoldani a feladatot. Ezek a megoldások nagy tesztesetekre nem mindig futottak le időben. Ennek ellenére, ügyes optimalizációkkal 9 pontot is el lehetett így érni. Ez a megoldás Nagy Miklós 12. osztályos győri versenyzőnek sikerült a legjobban.
Statistics:
7 students sent a solution. 10 points: Jules Pondard, Nagy Róbert. 9 points: Barta 111 János, Borsos 607 Zalán, Nagy 111 Miklós. 5 points: 1 student. 4 points: 1 student.
Problems in Information Technology of KöMaL, November 2010
