Problem S. 59. (January 2011)

S. 59. An investor plans to build a new luxury supermarket in the heart Manhattan. He knows that the building should be built as close to his future clients as possible. He already accurately surveyed the number of possible clients from each part of the city. Your task is to specify a location for the supermarket such that customers can reach it with the least travelling on the average.

Your program should solve this task. As usual, the map of Manhattan is considered as a regular grid with two-way streets, and crossings having integer coordinates.

For simplicity, we identify clients' flats and the supermarket with the corresponding nearest crossings. Instead of the Euclidean distance, we measure the distance between crossing $\mathbf{p}_{i}$ with coordinates (x_i,y_i) and crossing $\mathbf{p}_{j}$ with coordinates (x_j,y_j) by the following formula (which is often termed as Manhattan distance): $d(\mathbf{p}_i,\mathbf{p}_j)= |x_j -x_i|+ |y_j -y_i|$ , measuring the shortest distance along the grid.

The result of the investor's survey is read from the standard input: its first line contains the number of crossings $1\le N\le 1\;000\;000$ , and the following N lines describe each crossing. There are three integers in the (i+1)^st line separated by a space: the two coordinates $0\le x_i,y_i \le 1\;000\;000$ of the i^th crossing and the number of expected clients 1 $\le$ w_i $\le$ 1000 living there.

Your program should find the optimal crossing $\mathbf{p}_{0}$ such that the average weighted distance between $\mathbf{p}_{0}$ and all the crossings listed above is minimal (with weights being the number of clients living on the actual crossing). In other words, the quantity

$\overline D = \frac{\sum_{i=1}^N d(\mathbf{p}_0,\mathbf{p}_i)\cdot w_i}{\sum_{i=1}^N w_i}$

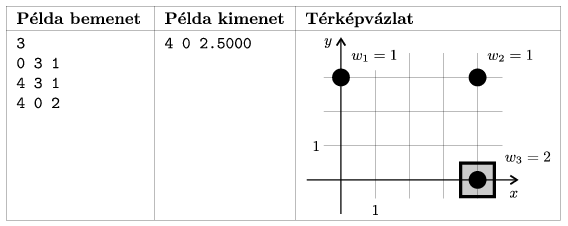
is to be minimized. The standard output should only contain three numbers separated by a space: the two coordinates x₀, y₀ of the optimal location $\mathbf{p}_{0}$ and the average weighted distance $\overline D$ with 4 digits of precision. If there are many solutions, any of them can be given. In the example, ``Példa bemenet'' is a sample input, ``kimenet'' is output, while ``Térképvázlat'' is the corresponding map.

Evaluation: the maximal 8 points can be awarded if your program solves the largest test cases within one minute. 5 points can be awarded if your program correctly handles test cases already with N $\le$ 1000. The documentation is worth 2 points.

The source code and project files of your solution -- without the .exe or any other auxiliary files generated by the compiler -- should be submitted together with a short documentation (s59.txt, s59.pdf, ...) in a compressed folder s59.zip.

(10 pont)

Deadline expired on February 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásvázlat

A megoldáshoz azt kellett észrevenni, hogy az átlagos távolság épp akkor minimális, amikor a súlyozott távolságösszeg minimális (hisz egymás konstansszorosai), ennek pedig függőleges és vízszintes összetevői egymástól teljesen függetlenek, így külön-külön minimalizálhatóak.

Tehát két egydimenziós problémát kaptunk: két, abszolútérték-függvények összegeiből felépített függvény minimumhelyét kell meghatároznunk. Az ilyen függvények konvexek, és egyenes szakaszokra bonthatóak: minimumhelyük tehát ott van, ahol ezen szakaszok meredeksége negatívból pozitívba fordul, amely egy rendezés után lineáris időben meghatározható.

C++ mintamegoldás

Statistics:

8 students sent a solution.

10 points: Borsos 607 Zalán, Nagy 111 Miklós, Szabó 928 Attila.

9 points: Nagy Róbert.

8 points: 1 student.

7 points: 1 student.

5 points: 1 student.

4 points: 1 student.

Problems in Information Technology of KöMaL, January 2011

8 students sent a solution.
10 points:	Borsos 607 Zalán, Nagy 111 Miklós, Szabó 928 Attila.
9 points:	Nagy Róbert.
8 points:	1 student.
7 points:	1 student.
5 points:	1 student.
4 points:	1 student.

Already signed up?
New to KöMaL?