 Problem S. 61. (March 2011)
Problem S. 61. (March 2011)
S. 61. In a typical alphanumeric problem digits are represented by letters: each letter represents a digit, the same letters denote the same digit, and different ones a different digit. One should find a possible value for these letters such that the resulting addition is a valid one, with the further restriction that the leading digit of the sum can not be 0.
For example, consider the alphanumeric problem \(\displaystyle \overline{emmsk} + \overline{massk} = \overline{eemee\vphantom{k}}\). Then there is a solution (and the solution is unique in this case): \(\displaystyle a=7\), \(\displaystyle e=8\), \(\displaystyle k=4\), \(\displaystyle m=0\), \(\displaystyle s=9\), because after substitution we get the following equality: \(\displaystyle 80094 + 07994 = 88088\).
You should write a program that reads an alphanumeric problem in a given base from the standard input, then gives a possible solution (if it exists) and the number of all solutions.
The structure of the input is the following: the first line contains the base of the number system (\(\displaystyle 2 \le b \le 23\), represented as a decimal number), the second and third lines contain the two addends, while the fourth line contains the sum. The last three lines contain only lowercase letters of the English alphabet and their length is at most 1000 characters.
The first line of the standard output should contain the number of solutions. If this is greater than zero, then the second line should contain an arbitrary solution in the format specified below. Each letter should be listed, separated by a space, together with an equation sign and the corresponding digit value. Digits with value greater than 9 are represented by successive uppercase letters of the English alphabet, similarly to the hexadecimal number system.
In the example, ``Példa bemenet'' is the input, while ``Példa kimenet'' is a possible output.

We remark that the complete solution set of this example is the following:
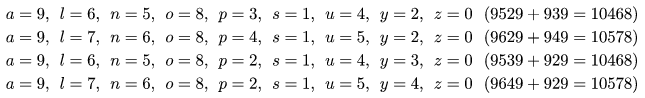
The time limit for your program is 1 minute in each test case.
The source code and project files of your solution (without the .exe file or any other auxiliary files generated by the compiler) should be submitted together with a short documentation in a compressed folder s61.zip.
You can obtain 8 points for this exercise if your program gives a correct answer to all test cases available on our web page, within the specified time limit. You may get a reduced number of points if your program does not give the number of solutions, or only able to work in the decimal system.
A further 2 points can be awarded for the documentation.
Downloadable files: s61.zip
(10 pont)
Deadline expired on April 11, 2011.
Sorry, the solution is available only in Hungarian. Google translation
A feladat elég nehéznek bizonyult. Csak két megoldás érkezett, és némelyik tesztesetre ezek sem futottak le időben.
A feladatot hátulról induló backtrack-el lehetett megoldani. A megoldás lényege a következő:
Kezdetben nincs semelyik betűhöz sem érték rendelve. A rekurzív függvényt először az utolsó pozícióra hívjuk meg. A függvény végigmegy a számrendszer összes számjegyén, és ha egy számjegy hozzárendelhető az aktuális pozíción lévő betűhöz, akkor elvégzi a hozzárendelést, meghívja önmagát a következő pozícióra, majd visszavonja a hozzárendelést.
Ennek az algoritmusnak a gyorsasága azon múlik, hogy mennyire hamar sikerül abbahagyni az olyan ágak vizsgálatát, amik már biztosan nem szolgáltatnak megoldást (azaz amikre valamelyik oszlopban hibás az összeadás). Természetesen adódik az a módszer, hogy amikor a rekurzió az i. oszlopból átlépne az i-1. oszlopba, akkor megnézi, hogy az összedás eredményének i. számjegye megfelel-e a behelyettesített értéknek. Azonban a 10 pontos megoldáshoz egy bonyolultabb vágási módszerre is szükség van.
Amikor rögzítjük egy betű értékét, előfordulhat, hogy ezzel valamelyik későbbi oszlopban már mindhárom számjegy értéke rögzítve van. Minden ilyen oszlopot rögtön megvizsgálhatunk, hogy nem kapunk-e ellentmondást. Mivel két számot adunk össze, ezért az átvitel csak 0 vagy 1 lehet, tehát ha az összeg megfelelő oszlopában lévő számejgyből levonva az összeadandókban lévő két számjegyet nem 0-t vagy 1-et kapunk, akkor már biztosan hibás a helyettesítésünk, tehát visszavonhatjuk az utolsó rögzítést, és nem kell rekurzív hívást csinálni.
Hosszú számok esetén ez jelentős gyorsítást jelent, ugyanis pl. egy 1000 hosszú számban 23-as számrendszer esetén átlagosan kb. 43-szor fordul elő minden számban mindegyik betű, vagyis sok lehetőség van hibás oszlop kialakulására.
Statistics:
2 students sent a solution. 9 points: Borsos 607 Zalán, Nagy 111 Miklós.
Problems in Information Technology of KöMaL, March 2011
