 |
Az S. 61. feladat (2011. március) |
S. 61. Az ún. betűösszeadás-feladványokban számjegyek helyett betűk szerepelnek. Az azonos betűk ugyanazt a számjegyet jelentik, a különbözőek különbözőeket. A betűk jelentését úgy kell megválasztani, hogy érvényes összeadást kapjunk. További kikötés, hogy az összeg első számjegye nem lehet nulla.
Például: \(\displaystyle \overline{emmsk} + \overline{massk} = \overline{eemee\vphantom{k}}\). Ennek a betű-összeadásnak egyetlen megoldása van: \(\displaystyle a=7\), \(\displaystyle e=8\), \(\displaystyle k=4\), \(\displaystyle m=0\), \(\displaystyle s=9\). Behelyettesítve a következő összeadást kapjuk: \(\displaystyle 80094 + 07994 = 88088\).
Írjunk programot, amely a standard bemenetről beolvas egy megadott számrendszerbeli betűösszeadás-feladványt, és megad egy megoldást (ha létezik), valamint azt, hogy hány megoldása van.
A bemenet szerkezete a következő: az első sorban a számrendszer alapszáma (\(\displaystyle 2 \le b \le 23\)) szerepel (számmal írva), a másodikban és a harmadikban a két összeadandó, a negyedikben pedig az összeg (mindben csak az angol ábécé kisbetűi szerepelnek, és hosszuk legfeljebb 1000 karakter).
A standard kimenet első sorában a megoldások száma szerepeljen. Amennyiben ez nem nulla, úgy a második sorban adjunk is meg egy tetszőleges megoldást, az alábbi formátumban. A bemenetben szereplő minden betűt soroljunk fel (szóközökkel elválasztva), és egyenlőségjellel kapcsolva írjuk melléjük a hozzárendelt számjegyet. A 9-nél nagyobb értékű számjegyeket rendre az angol ábécé nagybetűivel jelöljük, a hexadecimális számrendszerhez hasonlóan.

A példa összes megoldása:
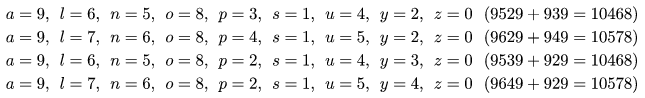
A futásidőlimit tesztesetenként 1 perc.
Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét röviden bemutató dokumentáció egy tömörített s61.zip mappában.
Értékelés: 8 pontot ér az a program, amely a honlapunkon elérhető mindegyik tesztesetre a megadott időkorláton belül helyes eredményt ad. Részpontszámok kaphatóak az olyan programra, amely nem adja meg a megoldások számát, vagy csak 10-es számrendszerbeli számokra működik. További 2 pont szerezhető a dokumentációval.
Példa bemenetek és példa kimenetek: s61.zip
(10 pont)
A beküldési határidő 2011. április 11-én LEJÁRT.
A feladat elég nehéznek bizonyult. Csak két megoldás érkezett, és némelyik tesztesetre ezek sem futottak le időben.
A feladatot hátulról induló backtrack-el lehetett megoldani. A megoldás lényege a következő:
Kezdetben nincs semelyik betűhöz sem érték rendelve. A rekurzív függvényt először az utolsó pozícióra hívjuk meg. A függvény végigmegy a számrendszer összes számjegyén, és ha egy számjegy hozzárendelhető az aktuális pozíción lévő betűhöz, akkor elvégzi a hozzárendelést, meghívja önmagát a következő pozícióra, majd visszavonja a hozzárendelést.
Ennek az algoritmusnak a gyorsasága azon múlik, hogy mennyire hamar sikerül abbahagyni az olyan ágak vizsgálatát, amik már biztosan nem szolgáltatnak megoldást (azaz amikre valamelyik oszlopban hibás az összeadás). Természetesen adódik az a módszer, hogy amikor a rekurzió az i. oszlopból átlépne az i-1. oszlopba, akkor megnézi, hogy az összedás eredményének i. számjegye megfelel-e a behelyettesített értéknek. Azonban a 10 pontos megoldáshoz egy bonyolultabb vágási módszerre is szükség van.
Amikor rögzítjük egy betű értékét, előfordulhat, hogy ezzel valamelyik későbbi oszlopban már mindhárom számjegy értéke rögzítve van. Minden ilyen oszlopot rögtön megvizsgálhatunk, hogy nem kapunk-e ellentmondást. Mivel két számot adunk össze, ezért az átvitel csak 0 vagy 1 lehet, tehát ha az összeg megfelelő oszlopában lévő számejgyből levonva az összeadandókban lévő két számjegyet nem 0-t vagy 1-et kapunk, akkor már biztosan hibás a helyettesítésünk, tehát visszavonhatjuk az utolsó rögzítést, és nem kell rekurzív hívást csinálni.
Hosszú számok esetén ez jelentős gyorsítást jelent, ugyanis pl. egy 1000 hosszú számban 23-as számrendszer esetén átlagosan kb. 43-szor fordul elő minden számban mindegyik betű, vagyis sok lehetőség van hibás oszlop kialakulására.
Statisztika:
2 dolgozat érkezett. 9 pontot kapott: Borsos 607 Zalán, Nagy 111 Miklós.
A KöMaL 2011. márciusi informatika feladatai

