Problem S. 86. (January 2014)

S. 86. There are N monkeys and a very large tree in a park. The first monkey is hanging from the tree by its tail. A monkey can connect to another one by grasping the other monkey's leg with one of its hands. In this way a monkey can hold other monkeys by connecting to them or the other monkeys can connect to it. An arbitrary number of monkeys can connect to the legs of a given one. We observe this monkey group for M seconds. In each second during the observation period, a monkey frees up a given hand, that is, it releases the leg of another monkey it was connected to. Your program should determine when a given monkey hits the ground. A monkey hits the ground, if it is no longer connected to the first monkey either in a direct or indirect way.

The first line of the standard input contains the number of the monkeys ( $1\le N\le 200\;000$ ) and the duration of the observation ( $1\le M\le 400\;000$ , in seconds). Then each of the next N lines contains two numbers 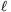$\ell$ _i and r_i, describing that the left and right hands of the $i^\mathrm{th}$ monkey, respectively, are connected to which monkey's leg. If any of these numbers is -1, then the actual monkey's actual hand is not connected to any monkey, and this hand does not hold any monkeys. The x_j, y_j pairs of integers in the next M lines of the standard input show that the y_j hand (``1'' is left and ``2'' is right) of monkey x_j releases the grasp in the $j^\mathrm{th}$ second. The N lines of the standard output should contain the time instants of the monkeys falling to the ground: the $i^\mathrm{th}$ line refers to the $i^\mathrm{th}$ monkey, and it contains -1 if this monkey did not fall down during the observation period. In the example, two sample inputs (``Példa bemenet'') and the corresponding outputs (``Példa kimenet'') are displayed.

Scoring and bounds. You can obtain 1 point for a brief and proper documentation clearly describing your solution. 9 further points can be obtained provided that your program solves any arbitrary valid input within 0.05 seconds of running time after loading the data.

Partial points can be obtained if your program yields a solution

- for N $\le$ 100;

- for N $\le$ 5000;

- for $N\le 50\;000$ .

The source code (s86.pas, s86.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (s86.txt, s86.pdf, ...), also describing which developer environment to use for compiling the source, should be submitted in a compressed file s86.zip.

(10 pont)

Deadline expired on February 10, 2014.

Sorry, the solution is available only in Hungarian. Google translation

Mintamegoldásnak Weisz Ambrus és Makk László megoldását tesszük közzé. Az alapötlet az, hogy időben visszafelé nézzük az eseményeket. Innentől egy szélességi bejárás megoldja. main.cpp

S86megoldas.txt

s86.zip

Statistics:

14 students sent a solution.

10 points: Makk László, Weisz Ambrus.

8 points: 1 student.

7 points: 3 students.

5 points: 1 student.

4 points: 2 students.

3 points: 1 student.

2 points: 1 student.

1 point: 1 student.

0 point: 2 students.

Problems in Information Technology of KöMaL, January 2014

14 students sent a solution.
10 points:	Makk László, Weisz Ambrus.
8 points:	1 student.
7 points:	3 students.
5 points:	1 student.
4 points:	2 students.
3 points:	1 student.
2 points:	1 student.
1 point:	1 student.
0 point:	2 students.

Already signed up?
New to KöMaL?