 Problem S. 94. (December 2014)
Problem S. 94. (December 2014)
S. 94. Some researchers discovered that the results of a particular animal experiment tend to be unreliable when too many animals get in contact with one another. At present there are too many animals in a square field of size \(\displaystyle N\times N\) (\(\displaystyle 2\le N\le 17\)). We want to build \(\displaystyle K\) (\(\displaystyle 1\le K\le 2N-2\)) fences to separate them. A fence always runs parallel with one of the field edges, and the distance between them is an integer. Moreover, a fence passes through the square completely, that is, a fence cannot end in the square interior. Given the above constraints, by suitably building fences we would like to minimize the maximum number of animals in any connected part.
Your program should read the values of \(\displaystyle N\) and \(\displaystyle K\) (\(\displaystyle 2\le N\le 17\), \(\displaystyle 1\le K\le 2N-2\)) from the first line of the standard input; then \(\displaystyle N\) integers from each of the following \(\displaystyle N\) lines, describing for each row the number of animals in each of the \(\displaystyle N\) unit squares of that row. The first and only line of the standard output should contain the maximum number of animals that are not separated from each other, provided that the best fence-building strategy was used.
In the example, ``Példa bemenet'' is a sample input, and ``Példa kimenet'' is the corresponding output.
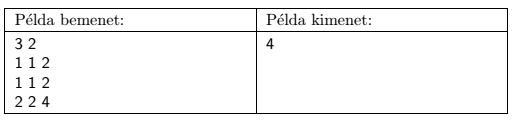
Explanation: we have to build two fences. We build the first fence between the 2nd and the 3rd columns, and the second fence between the 2nd and the 3rd rows. Then the upper left area will contain \(\displaystyle 1+1+1+1=4\) animals, the upper right area will have \(\displaystyle 2+2=4\), the lower left area \(\displaystyle 2+2=4\), and the lower right area will have 4 animals, so we display 4 as an output.
Scoring and bounds. You can obtain 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any arbitrary valid input within 1 second of running time.
The source code (s94.pas, s94.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (s94.txt, s94.pdf, ...), also describing which developer environment to use for compiling the source, should be submitted in a compressed file s94.zip.
(10 pont)
Deadline expired on January 12, 2015.
Statistics:
7 students sent a solution. 10 points: Gáspár Attila. 6 points: 1 student. 5 points: 1 student. 4 points: 1 student. 2 points: 3 students.
Problems in Information Technology of KöMaL, December 2014
