Problem S. 97. (March 2015)

S. 97. Elephants in a herd are walking calmly in a single line. Elephants are numbered from 1 to \(\displaystyle N\) (\(\displaystyle 1\le N\le 100\;000\)). Elephant 1 is the smallest one, then gradually, Elephant \(\displaystyle N\) is the largest animal of them. It would be nice to have the smallest elephant in the first place, then the second smallest, and so on. However, currently they are not necessarily in this order. We say that a pair of elephants from the line is in wrong order, if the larger animal precedes the smaller. You should determine the number of pairs in wrong order.

Your program should read the value of \(\displaystyle N\) from the first line of the standard input, then \(\displaystyle N\) numbers from the next line denoting the elephants in the line. The first and only line of the standard output should contain the number of elephant pairs in wrong order.

In the example, ``Példa bemenet'' is sample input, while ``Példa kimenet'' is the corresponding output.

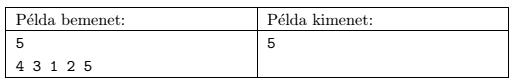
Explanation: the pairs (1,3), (1,4), (2,3), (2,4) and (3,4) are in wrong order.

Scoring and bounds. You can obtain 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any arbitrary valid input within 1 second of running time.

The source code (s97.pas, s97.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (s97.txt, s97.pdf, ...), also describing which developer environment to use for compiling the source, should be submitted in a compressed file s97.zip.

(10 pont)

Deadline expired on April 10, 2015.

Statistics:

15 students sent a solution.
10 points:	Alexy Marcell, Csenger Géza, Gergely Patrik, Kiss Gergely, Németh 123 Balázs.
9 points:	Gáspár Attila, Molnár-Sáska Zoltán, Weisz Ambrus, Zarándy Álmos.
8 points:	1 student.
6 points:	3 students.
5 points:	1 student.
2 points:	1 student.

Problems in Information Technology of KöMaL, March 2015