 Problem S. 99. (May 2015)
Problem S. 99. (May 2015)
S. 99. We notice that \(\displaystyle N\) cracks (\(\displaystyle 1\le N\le 5000\)) appeared on a wall of length \(\displaystyle M\) (\(\displaystyle 1\le M\le 100\;000\), with integer \(\displaystyle M\)). In this exercise, cracks are modeled as points, and their location is given by some integer coordinates \(\displaystyle x\) (\(\displaystyle 1\le x\le M\)) measured from one end of the wall. Our goal is to cover all cracks on the wall with paint.
By opening a bucket of paint labeled ``\(\displaystyle w\)'', we can paint a wall segment of length exactly \(\displaystyle w\), bounded by the coordinates \(\displaystyle x_0\) and \(\displaystyle x_1\) (\(\displaystyle w=x_1-x_0+1\)). Within this wall segment we can of course cover the intact parts of the wall as well, even multiple times. We keep on opening the buckets and painting until all cracks are covered. For each integer \(\displaystyle w\) (\(\displaystyle 1\le w\le M\)), we have one bucket of paint labeled ``\(\displaystyle w\)'' and with known cost \(\displaystyle b_j\). Painting a longer wall segment may cost less than painting a shorter one; and it may also happen that the price of a bigger bucket is less than or equal to the price of a smaller bucket. Your task is to cover all cracks on the wall for the minimum cost.
Your program should read the values of \(\displaystyle N\) and \(\displaystyle M\) from the first line of the standard input, then the \(\displaystyle a_i\) integers (describing the crack locations) from the following \(\displaystyle N\) lines. The next \(\displaystyle M\) lines contain the paint bucket prices \(\displaystyle b_j\) corresponding to the consecutive lengths. The first line of the standard output should contain the minimum cost necessary to complete the wall painting. To save space, instead of displaying numbers in \(\displaystyle N\) and \(\displaystyle M\) input lines, they appear in one line and are separated with / characters.
In the example, ``Példa bemenet'' is a sample input, while ``Példa kimenet'' is the corresponding output. In this situation, 3 paint buckets with labels ``4'', ``1'' and ``2'' are sufficient to paint all the cracks; the cost is \(\displaystyle 4+2+3=9\).
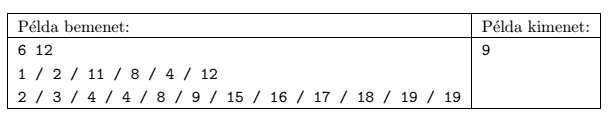
Scoring and bounds. You can obtain 1 point for a brief and proper documentation clearly describing your solution. Nine further points can be obtained provided that your program solves any arbitrary valid input within 1 second of running time.
The source code (s99.pas, s99.cpp, ...) without the .exe or any other auxiliary files generated by the compiler but with a short documentation (s99.txt, s99.pdf, ...), also describing which developer environment to use for compiling your source, should be submitted in a compressed file s99.zip.
(10 pont)
Deadline expired on June 17, 2015.
Statistics:
8 students sent a solution. 10 points: Gáspár Attila. 9 points: Németh 123 Balázs. 8 points: 1 student. 7 points: 1 student. 6 points: 2 students. 5 points: 1 student. 1 point: 1 student.
Problems in Information Technology of KöMaL, May 2015
