KöMaL Problems in Physics, April 2005
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on May 11, 2005. |
M. 260. It is well known that a glass placed under a strong water jet cannot be filled entirely. Removing the glass from under the jet it will only be partly filled with water. How does the amount of the remaining water in the glass depend on the flow rate, the velocity of the jet and the position of the glass?
(6 pont)
 |
Problems with sign 'P'Deadline expired on May 11, 2005. |
P. 3792. A collecting lens makes a 6 cm high real image of a 12 cm high object on a screen at a 45 cm distance from the object. Determine the position of the lens and its focal length with plotting and calculation.
(4 pont)
P. 3793. In theory at the North and South Poles days and nights last for exactly half a year. In fact, the length of a day (the time between sunrise and sunset) is about 2 weeks longer in both places. Why?
(4 pont)
P. 3794. In an experimental device where controlled nuclear fusion is generated, a solid-state laser emits infrared light in 1.1.10-11 s at the wavelength of 1060 nm with a power of 1014 W. For comparison: a school He-Ne laser emits red light at the wavelength of 633 nm with a power of 10-3 W. For how many days should the He-Ne laser work to emit the same number of photons as the solid-state laser does in 1.1.10-11 s?
(3 pont)
P. 3795. We have to cool down a 5 kg copper block of a temperature of 300 oC to the temperature of 30 oC. We can use 20 oC water for the cooling supplied at an arbitrary rate. At what rate is the cooling water to be used so that the smallest possible amount of water is used for the cooling? How much is this quantity? (Let us assume that the temperature of the copper block changes only as a result of the effect of the water poured on it.)
(5 pont)
P. 3796. On a slope of height h a small body is sliding down without friction. It is connected to a point P at the bottom of the slope with a push-and-pull spring of an elastic constant of D, which was initially not extended. The body just stops at the bottom of the slope. What can the slope angle  be? What is the acceleration when the body of mass m starts sliding back?
be? What is the acceleration when the body of mass m starts sliding back?
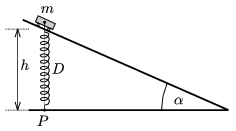
(5 pont)
P. 3797. On a horizontal frictionless table a stick of mass M, length of L and of homogeneous mass distribution is standing.
a) With what velocity had a small body of mass m slid into it, if the stick hit the table after a turn of an angle  ?
?
b) How far was the mass center of the stick from the small body at this moment?
(The collision of the small body and the stick is perfectly elastic.) (Data: M=0.6 kg, m=0.2 kg, L=0.8 m,  =60o.)
=60o.)
(5 pont)
P. 3798. A 0.8 m long rod joins to a vertical axle with a bearing at its middle. The rod has negligible mass and it is frictionless. We thread point-like pierced balls of masses of 200 g on both of its ends. The two balls positioned symmetrically on both sides of the axis are linked with a thin thread of a length of 0.2 m. At the ends of the rod there are non-elastic bumpers. We spin this system with an angular velocity of 2 s-1 and then we burn the thread.
a) What path do the balls follow?
b) How much does the rod turn in 1 s after burning the fibre.
c) In what time does the rod turn by an angle of 180o?
d) What distance is done by the balls during the half turn of the rod?
e) What percentage is the mechanical loss?
(5 pont)
P. 3799. We touch a charged metal sphere of a radius of R with an uncharged metal sphere of a radius of r and then the two are properly separated. Then we touch the previous metal sphere of radius R with another uncharged metal sphere of a radius of also R. After this we arrange the three metal spheres at proper distances from each other in the points of a regular triangle. What is the direction of the electric field strength in the middle of the triangle?
(4 pont)
P. 3800. A metal ring having three metallic spokes of lengths r=0.2 m is in a vertical plane and can spin around a fixed horizontal axis in a homogeneous magnetic field of a magnetic induction of B=0.5 T. The lines of magnetic field are perpendicular to the plane of the metal ring. Between the axis of the metal ring and its perimeter we connect a consumer of a resistance of 0.15  with the help of two sliding contacts. We fix a thread of negligible mass to the rim of the ring and wind it several times around the ring and to its end we fix a body of a mass of 20 g. At a given moment we release the body of mass m. The friction is negligible everywhere, the resistance of the ring, the spokes and the connected wiring is also negligible.
with the help of two sliding contacts. We fix a thread of negligible mass to the rim of the ring and wind it several times around the ring and to its end we fix a body of a mass of 20 g. At a given moment we release the body of mass m. The friction is negligible everywhere, the resistance of the ring, the spokes and the connected wiring is also negligible.
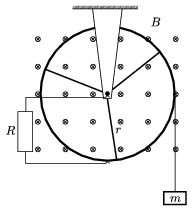
a) What is the torque exerted on the ring with the spokes by the magnetic forces when the body of mass m is moving with a constant velocity?
b) What current is flowing through the consumer when the velocity of the body of mass m is 3 m/s?
c) What is the highest velocity of the body of mass m?
(4 pont)
P. 3801. What is the difference between the 3 cm wavelength component of the cosmic background radiation and the same wavelength microwave radiation of the telecommunication satellites?
(4 pont)
P. 3802. What voltage is connected to the plane capacitor in vacuum, the plates of which are at 1 cm distance from each other, when the electrons detaching from the negative plate impact to the positive one with a velocity that is 60% of the speed of light. Solve the problem with both relativistic and non-relativistic methods.
(4 pont)
Upload your solutions above.
