A KöMaL 2005. áprilisi informatika feladatai

I-jelű feladatok A beküldési határidő 2005. május 17-én LEJÁRT.

I. 103. Kísérletezzünk, gondolkozzunk!

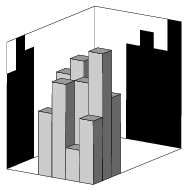
Van egy mxn-es négyzetrácsunk (m és n pozitív egész számok), melynek egyes négyzeteire egységnégyzet alapú hasábot állítottunk. A test elöl-, illetve oldalnézeti képe (árnyéka) oszlopdiagram-szerű lesz. Az egyes téglalapok magasságát az u₁, u₂, ..., u_m és v₁, v₂, ..., v_n számokkal adjuk meg.

Írjunk programot, amelybe inputként beírva az m, n, u₁, u₂, ..., u_m és v₁, v₂, ..., v_n számokat az I. 100. feladatban leírt formában, kiszámítja az azokhoz tartozó (egyik) minimális térfogatú testet leíró mátrixot - vagy kiírja, hogy nem létezik ilyen test, és jelölje meg azokat az adatokat, amelyek miatt nincs ilyen test.

Feladatunk az I. 98.-as feladat egy megfordítása: ott az oszlopokból álló testet egyértelműen megadó mátrixból kellett meghatározni a vetületeket, most a vetületekből kell meghatározni a lehetséges legkisebb testet.

Beküldendő egy TEXT fájl (i103.txt), amely tartalmazza az algoritmus pontos leírását (5 pont) és annak részletes indoklását, hogy a leírt algoritmus minden esetben jól dönti el, hogy van-e adott tulajdonságú test, és ha van, az algoritmus valóban a kívánt tulajdonságú testet adja meg (8 pont), valamint a program (4 pont) (i103.pas, ...).

(17 pont)

statisztika

I. 104. Kísérletezzünk, gondolkozzunk!

Adott egy n pozitív egész szám. Van-e olyan n darab pozitív egész szám, amelynek összege ugyanannyi, mint a szorzatuk?

Írjunk olyan programot (i104.pas, ...), amely választ ad erre a kérdésre, és ha van megoldás, akkor adja meg az összes lehetséges szám-n-est, a számok növekvő sorrendjében.

Beküldendő a program (i104.pas, ...).

(10 pont)

statisztika

I. 105. Egy kutyakiállításon n kategóriában m kutyát pontoznak: minden kutya minden egyes kategóriában egy-egy pontszámot kap (0-10 pont, egész szám), amit a versenybizottság azonnal beleír egy táblázatkezelőbe. A bizottság (nem matematikus) elnöke azt kéri, hogy a táblázatkezelő jelezze ki, hogy az (összpontszám szerint) abszolút győztes kutya hány kategóriában nyert.

Beküldendő a táblázat (i105.xls).

(10 pont)

statisztika

S-jelű feladatok A beküldési határidő 2005. május 17-én LEJÁRT.

S. 8. Írjunk porgramot, amely az amőba játékban, 15x15-ös táblán, egy tetszőleges állásban lépést javasol.

A program a standard bemenetről olvassa be az állást. Az üres mezőket, a gép és az ellenfél bábuit a ., O, illetve X karakterek jelölik. A legjobbnak tartott lépést a standard kimenetre írja ki. A sorokat az A, ..., O betűkkel, az oszlopokat az 1, ..., 15 számokkal jelölje. (Például a harmadik sor kilencedik mezőjének jele C9.)

A megoldásokat 2GHz-es gépen fogjuk tesztelni, a lépést 10 másodpercen belül ki kell írni. A működő programok között körmérkőzést rendezünk, a győztes (megfelelő dokumentáció esetén) 10 pontot kap, a második helyezett 8-at, a többi megoldás legfeljebb 7-et kaphat.

Figyelem! Kizárólag a versenykiírásban felsorolt nyelveken írt programokat (Pascal, C/C++, Java) fogadjuk el! A program ne rajzoljon, ne törölje le a képernyőt, ne olvasson fájlból és ne írjon fájlba, és a lépésen kívül semmi mást ne írjon ki!

Példa:

............... 
...............
...............
...............
...............
...............
......O........
......XXX......
.......O.......
...............
...............
...............
...............
...............
...............
...............

(10 pont)

statisztika