KöMaL Problems in Mathematics, May 2005
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'C'Deadline expired on June 15, 2005. |
C. 810. Find those three-digit numbers divisible by 45 in which the digits (in that order) form an arithmetic progression.
(5 pont)
solution (in Hungarian), statistics
C. 811. Find those consecutive integers that add up to 100.
(5 pont)
solution (in Hungarian), statistics
C. 812. A steam locomotive is going to Kanizsa from Zalakomár that is 21 km away. The journey takes 16 minutes. The locomotive accelerates uniformly to 90 km/h, then continues at constant speed, and then decelerates uniformly to rest. How long is it travelling at constant speed?
(5 pont)
solution (in Hungarian), statistics
C. 813. One side of a rectangle is 10 cm long. How long is the other side if a 10 cm x1 cm rectangle can be just placed in it in a diagonal position?
(5 pont)
solution (in Hungarian), statistics
C. 814. Solve the following simultaneous system with a t real parameter:
x+y+z=t,
x+(t+1)y+z=0,
x+y-(t+1)z=2t.
(5 pont)
 |
Problems with sign 'B'Deadline expired on June 15, 2005. |
B. 3822. Is it possible to obtain the array (1,3,8) starting from (2,5,13) by repeating the following steps: It is allowed to swap any two numbers in an array of three numbers (a,b,c), or replace the array by (a,b,2a+2b-c).
(4 pont)
solution (in Hungarian), statistics
B. 3823. Let x and y denote integers, such that 4x + 5y =7. Find the smallest value of 5|x|-3|y|.
(3 pont)
solution (in Hungarian), statistics
B. 3824. Each vertex of a tetrahedron is reflected in the centroid of the opposite face. Show that the volume of the tetrahedron formed by the reflections is at least four times that of the original tetrahedron.
(4 pont)
solution (in Hungarian), statistics
B. 3825. n is a positive integer, such that 2n+1 and 3n+1 are both square numbers. Prove that n is divisible by 40.
(4 pont)
solution (in Hungarian), statistics
B. 3826. What kind of quadrilateral is the base of the truncated pyramid if every pair of space diagonals of the solid intersect each other?
(4 pont)
solution (in Hungarian), statistics
B. 3827. The line segment AD touches the circumscribed circle of the triangle ABC, and the line segment AC touches that of the triangle ABD. Prove that AC2.BD=AD2.BC.
(4 pont)
solution (in Hungarian), statistics
B. 3828. Is it true that if the product of the sides of a quadrilateral equals the square of its area then the quadrilateral has at least two right angles?
(4 pont)
solution (in Hungarian), statistics
B. 3829. Let a1, a2, ..., an denote positive numbers. Prove that
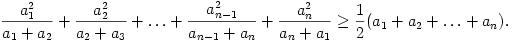
(5 pont)
solution (in Hungarian), statistics
B. 3830. Consider the centres of the squares ABDE and BCGH drawn inside above the sides AB and BC of a triangle ABC, and consider the midpoints of the line segments AC and DH. What is the shape formed by these four points?
(5 pont)
solution (in Hungarian), statistics
B. 3831. There is a square of side 2005 units long drawn on squared paper. The sides of the square are lattice lines. Draw a closed non self-crossing polygon inside the square, such that each side of the polygon is drawn along a lattice line, and it passes through every lattice point inside or on the boundary of the square exactly once. Show that the area bounded by the polygon is more than half the area of the square.
(5 pont)
 |
Problems with sign 'A'Deadline expired on June 15, 2005. |
A. 374. The real numbers x1 x2
x2 ...
... xn>0 and y1
xn>0 and y1 y2
y2 ...
... yn>0 satisfy
yn>0 satisfy
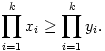
for all 0<k n. Prove that
n. Prove that
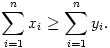
(5 pont)
A. 375. Find all continuous functions 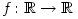 , such that
, such that
f (x+y+f(xy))=xy+f(x+y).
for all x,y  R.
R.
(5 pont)
A. 376. Is it possible to obtain the array (5,13,42) starting from (1,21,42) by repeating the following steps: It is allowed to swap any two numbers in an array of three numbers (a,b,c), or replace the array by (a,b,2a+2b-c).
(5 pont)
Upload your solutions above.
