KöMaL Problems in Informatics, September 2005
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on October 17, 2005. |
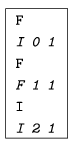
I. 109. Write a program to play the following game. The user enters ``head'' or ``tail'' in every step, which your program should guess in advance. The program should also make a statistics of its scores.
More precisely, the program reads the user's choice from the standard input, being a single letter H or T followed by an Enter. Then the program prints in one line its guess made beforehand, further, the number of its correct and incorrect guesses so far. The game is aborted by the user.
The program should make a record of the user's habits and make its decisions accordingly: the program should collect that -- depending on the last two steps and the program's guesses (being altogether 16 cases) -- heads or tails were entered more often by the user. (For example, if the user entered heads in the last two steps and the computer guessed them both correctly, then the program should examine the user's reaction in previous such situations whether heads or tails were selected more often.) If a given situation did not happen previously, or the user selected the same number of heads and tails, then the computer should guess randomly.
Example (messages from the computer are in italics):
The source code of your program (i109.pas, i109.c, ...) should be submitted.
(10 pont)
solution (in Hungarian), statistics
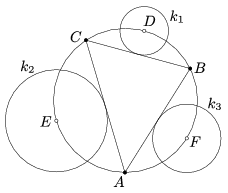
I. 110. Using the program Euklides, create and examine the following geometric configuration. Let a triangle ABC be given by its vertices. Let D denote the midpoint of the arc BC of the circumcircle of the triangle not containing A. The points E and F are defined analogously. Let k1 denote the circle centered at D and touching side BC. The circles k2 and k3 centered at E and F respectively are defined similarly.
Draw the common outer tangent lines of circles k1 and k2, k1 and k3, finally k2 and k3 (two tangent lines for each pair, altogether 6 lines). What conclusions can be drawn in the resulting figure?
You should submit the figure in Euklides's own file format (i110.euk), further, your geometric observations -- without proof -- in text format (i110.txt,
i110.rtf, ...). The Euklides figure should contain exactly 3 base points A, B and C. We should have a correct figure in every configuration of the base points, apart from the cases when the triangle is isosceles or the three points are collinear.
(10 pont)
solution (in Hungarian), statistics
I. 111. Let us demonstrate long multiplication by multiplying two 3-digit numbers.
Prepare an Excel sheet so that one can enter two integers with 3 digits (each digit in a separate cell) into a specific place in the first row. The next few rows should contain the progress and the result of the long multiplication of these numbers. You can assume that the numbers in fact have 3 digits, so, for example, no first digit can be 0.
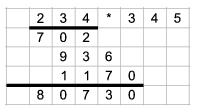
The sheet (i111.xls) is to be submitted.
(10 pont)
 |
Problems with sign 'S'Deadline expired on October 17, 2005. |
S. 10. Write a program that fills out a 3×3 magic square if some of its entries are given. (A magic square is a square array of numbers such that the sum of numbers in any horizontal, vertical and main diagonal line is always the same number.)
The program should read the initial state of the square from the standard input. Entries of the square will be given in three lines and separated by spaces. The numbers given in advance will be integers having at most 3 digits, while unspecified entries will be denoted by an X. Your program should display the resulting magic square in the same format on the standard output. Fractions in the output should be rounded to two decimal places.
It is of course possible that the given numbers are inconsistent and the magic square can not be completed. In this case your program should report ``No solution''. Similarly, it may happen that there are more than one (even infinitely many) solutions. In such cases the program should choose and display one possible solution and issue a warning ``The solution is not unique'' in the next line.

(10 pont)
$Var(Body)
Upload your solutions above
