KöMaL Problems in Physics, October 2005
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on November 11, 2005. |
M. 263. Fill the washbasin with some water, wait until the water has a smooth surface than (using a rope or a chain) suddenly pull out the plug and let the water drain away. Measure the time while the washbasin is emptied, as a function of the amount of water. Endeavour to investigate both cases: when there is, and there is no whirl in the water.
(6 pont)
 |
Problems with sign 'P'Deadline expired on November 11, 2005. |
P. 3824. Two carts are connected with a piece of rope and stay at rest on a horizontal tabletop. Their masses are m1 and m2. A highly compressed spring is placed between the carts. (The rope keeps the spring in the compressed state.) Than the rope is burnt, and the m1 mass moves with an initial speed of v1. Find the energy stored in the spring.
(3 pont)
P. 3825. By what amount does the area of a 20-Forint coin increase, if its diameter at 20 oC is 26.3 mm, and in our pocket its temperature increases to 35 oC. (The coefficient of linear expansion is  =1.84.10-5 oC-1.)
=1.84.10-5 oC-1.)
(3 pont)
P. 3826. A sample of diatomic ideal gas is confined in a 100 ml container at a pressure of 200 kPa. The average kinetic energy of a molecule is 5.10-20 J. Find the number of molecules and the number of moles of the gas in the container.
(3 pont)
P. 3827. Can the rate of energy transfer in the storage (rechargeable) battery decrease if switch K is turned on. Under what conditions does the power in the battery remain the same?
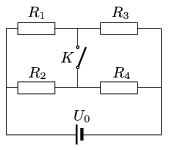
(4 pont)
P. 3828. A coin is observed from a distance of 22 cm.
a) What is the distance between the observer's eye and the image of the coin if a 5-dioptre lens is placed 10 cm away from the eye of the observer.
b) By what factor is the image of the coin observed through the lens and formed on the retina is greater than the image formed on the retina when the lens is not used.
c) Where should the lens be placed if we want the greatest image on the retina?
(5 pont)
P. 3829. A stone is thrown from the top of a vertical column at a certain angle above the horizontal. It strikes the ground twice as far as it would have struck it if it had been thrown from the bottom of the column with the same initial velocity. In this latter case the stone would fly during a time T. Find the height of the column.
(4 pont)
P. 3830. A small engine, fixed to a vertical wall at a height of H, winds up a piece of thread with a constant speed of v0. At the other end of the thread there is a small body which moves along the horizontal ground (friction is not negligible). How far is the small body from the wall when it rises from the ground? Data: H=20 cm, v0=5 cm/s.
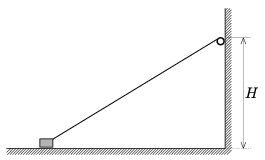
(5 pont)
P. 3831. A lasso made of a piece of metal wire is thrown around a stake fixed in the ground, and then the end of the lasso is pulled with a constant speed. Suppose that the loop around the stake remains circular. Calculate the induced current in the loop.
(5 pont)
P. 3832. At what speed should we move towards the red traffic-light in order to observe the light green?
(4 pont)
P. 3833. Can three point-like objects of different masses move in the gravitational fields of each other, such that the distances between any two are equal and remain constant during the motion? What is the angular speed of this rotating system?
(5 pont)
Upload your solutions above.
