KöMaL Problems in Mathematics, November 2005
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on December 12, 2005. |
K. 55. There are two milk bars in Cowton, and both of them have hot chocolate with frothed chocolate topping on their menus. Each milk bar serves in a cylindrical glass of the same height. (On serving, one half of the volume of the drink is liquid chocolate, and the other half is frothed chocolate.) In a short time, the froth turns into liquid chocolate of one quarter as much volume. In the Jolly Cowboy, chocolate is served in glasses of radius 6 cm, and sold for 12 Cowton cents a glass. In the Happy Cowgirl, the radius of the glasses is 5 cm, but they fill up the glass again when the froth of the first filling has settled. They charge 11 Cowton cents for a glass. In which milk bar is chocolate cheaper? [To obtain the volume of a cylinder, the area of its base is multiplied by its height.] (Based on a problem of the 24th József Öveges Memorial Competition)
(6 pont)
solution (in Hungarian), statistics
K. 56. Eskimos greet each other by rubbing their noses together, and they greet the members of an arctic expedition by a tap on the hand. The members of the expedition say hello to each other as well as to the Eskimos. At a certain event, ``Hello'' was said 415 times. How many nose rubbings and how many taps on the hand were there? (Everyone greeted everyone else in the appropriate way.)
(6 pont)
solution (in Hungarian), statistics
K. 57. A company had its logo designed. The designer drew the following sketch containing two different regular hexagons: Then he used the sketch to draw the final version. What is the ratio of the grey area to the area shaded with lines (in the second drawing)?
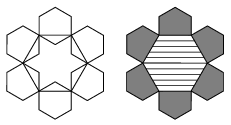
(6 pont)
solution (in Hungarian), statistics
K. 58. How many factors of 857 304 000 are perfect squares?
(6 pont)
solution (in Hungarian), statistics
K. 59. A circular table is put into the corner of a room. The diagram shows the table from above. The diameter of the tabletop is 170 cm. A certain point of the edge of the table is at a distance of 10 cm from one of the walls. Calculate its distance from the other wall.
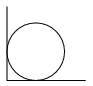
(6 pont)
solution (in Hungarian), statistics
K. 60. The structure shown in the diagram was obtained by glueing identical cubes together. Two cubes may be glued together only if their joining faces overlap to some extent (that is, it is not enough if they meet in an edge). Find the minimum number of cubes needed to build the structure in the diagram.
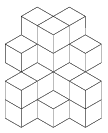
(6 pont)
 |
Problems with sign 'C'Deadline expired on December 15, 2005. |
C. 825. Prove that the product of four consecutive integers can always be expressed as the product of two consecutive even numbers.
(5 pont)
solution (in Hungarian), statistics
C. 826. Solve the following equation:
(5 pont)
solution (in Hungarian), statistics
C. 827. You are sitting in an aeroplane. Looking through a window 20 cm from your eye, you can see two boats in the direction of each of the lower corners of the 25 cm×40 cm window, respectively. Given that the plane is flying at an altitude of 10.3 km, and your eye is level with the horizontal bimedian of the window, determine the distance between the two boats.
(5 pont)
solution (in Hungarian), statistics
C. 828. Find the area of the triangle bounded by the lines
(5 pont)
solution (in Hungarian), statistics
C. 829. The five numbers drawn in the lottery of 10 September, 2005 were as follows: 4, 16, 22, 48, 88. All the five numbers are even, exactly four of them are divisible by four, three are divisible by 8 and two by 16. In how many different ways is it possible to select five numbers out of the whole numbers 1 to 90?
(5 pont)
 |
Problems with sign 'B'Deadline expired on December 15, 2005. |
B. 3852. a, b are integers, such that and
. Prove that
.
(3 pont)
solution (in Hungarian), statistics
B. 3853. Construct by ruler and compass a line of a given direction that halves the area of a given triangle.
(4 pont)
solution (in Hungarian), statistics
B. 3854. Is there a triangle, such that the triangle formed by its medians is similar to the triangle?
(4 pont)
solution (in Hungarian), statistics
B. 3855. What is the smallest possible number of acute-angled triangles that can be put together without gaps or overlaps to form an isosceles triangle with an apex angle of 120o?
(4 pont)
solution (in Hungarian), statistics
B. 3856. Show that if a2+b2=a2b2, and |a|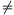 1, |b|
1, |b|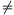 1, then
1, then
(3 pont)
solution (in Hungarian), statistics
B. 3857. One base and the two legs of a trapezium each have unit length. What should be the length of the other base so that the trapezium has the largest possible area?
(4 pont)
solution (in Hungarian), statistics
B. 3858. There are traffic lights at eight junctions along a main road. The probability that a certain light is red when one arrives there is 0.4. What is the probability that a car travelling down the road is not stopped by red lights at two consecutive junctions?
(4 pont)
solution (in Hungarian), statistics
B. 3859. Find all natural numbers n greater than 1, for which there is an order a1,a2,...,an of the numbers 1,2,3,...,n, such that the products a1, a1a2, a1a2a3, ..., a1a2...an divided by n all leave different remainders.
(5 pont)
solution (in Hungarian), statistics
B. 3860. The ``length'' of an elliptical tabletop is 160 cm and its ``width'' is 1 m. Is it possible to cover the table completely with a 140 cm×130 cm tablecloth?
(5 pont)
solution (in Hungarian), statistics
B. 3861. Prove that the only real root of the equation x7-14x6+21x5-70x4+35x3-42x2+7x-2=0 is .
Suggested by B. Kovács, Szatmárnémeti
(5 pont)
 |
Problems with sign 'A'Deadline expired on December 15, 2005. |
A. 383. The diameter AB of the circle k is perpendicular to the line  , which does not pass through either A or B. Let C be a point of
, which does not pass through either A or B. Let C be a point of  outside k, and let D denote the other intersection of the line AC with the circle. Draw one of the tangents from C to k and denote the point of contact by E. Let F be the intersection of the lines BE and
outside k, and let D denote the other intersection of the line AC with the circle. Draw one of the tangents from C to k and denote the point of contact by E. Let F be the intersection of the lines BE and  , and finally let G denote the intersection of the line segment AF with k. Show that the line DF passes through the reflection of the point G about AB.
, and finally let G denote the intersection of the line segment AF with k. Show that the line DF passes through the reflection of the point G about AB.
Based on a problem from Germany, suggested for the IMO
(5 pont)
A. 384. a0,a1,...,an and b0,b1,...,bk are non-negative real numbers, such that a0=b0=1 and (a0+a1x+...+anxn)(b0+b1x+...+bkxk)=1+x+...+xn+k. Prove that each of the numbers ai and bi is either 0 or 1.
IMC 2001, Prague
(5 pont)
A. 385. Find all sequences a1,a2,... of non-negative numbers, such that the sum is finite and
for all positive integers n.
(5 pont)
Upload your solutions above.
