A KöMaL 2005. decemberi informatika feladatai

I-jelű feladatok A beküldési határidő 2006. január 16-án LEJÁRT.

I. 118. Van n perselyünk és mindegyikhez egy-egy kulcsunk. Minden egyes kulcs csak a hozzá tartozó perselyt nyitja. Véletlenszerűen bedobáljuk a kulcsokat a perselyekbe, mindegyikbe egyet. Ezután t perselyt feltörünk. Mennyi a valószínűsége, hogy a feltört perselyekben levő kulcsokkal a többit már törés nélkül ki tudjuk nyitni? Írjunk programot, amely elvégez k számú kísérletet, és ez alapján megbecsüli a keresett valószínűséget. Ha n<10, akkor az összes eset megvizsgálásával számoljuk ki a pontos valószínűséget is.

A program a billentyűzetről olvassa be n, t és k értékét, végezze el a kísérleteket, majd írja ki az eredményül kapott relatív gyakoriságot (a sikeres kísérletek számát k-val osztva) és a pontos valószínűséget.

Beküldendő a program forráskódja (i118.pas, i118.cpp, ...).

(10 pont)

statisztika

I. 119. Készítsünk animációt Comenius Logo, PC Logo vagy NetLogo programmal, ami Botvinnik és Capablanca híres sakkpartiját mutatja be, amit az 1938-as AVRO versenyen játszottak.

A sakktábla mérete 560×560 legyen, a figurákat egy-egy teknőc lenyomataként állítsuk elő.

Beküldendő az elkészített Logo projekt (i119.lgp), ami tartalmazza az animációt futtató sakk nevű eljárást.

(10 pont)

megoldás, statisztika

I. 120. S forint kölcsönt veszünk fel kamatos kamatra. A kamat havonta p százalék, a futamidő n hónap. A kölcsönt havonta, egyenlő részletekben fizetjük vissza; az első részletet az első, az n-edik részletet az n-edik hónap végén. A bank a törlesztőrészletek befizetése előtt tőkésít, azaz adósságunk a kamatlábnak megfelelő mértékben növekszik, ezután vonják le belőle a befizetett összeget, végül nemnegatív egészre kerekítik -- mindig felfelé.

Készítsünk OpenOffice vagy Excel táblázatot, ami összesítést készít adósságunk alakulásáról. A felhasználó az A2, B2 és C2 mezőkbe írja be a kölcsön induló összegét (S), a kamatlábat (p), illetve a futamidőt (n). Az E2 mezőben jelenjen meg a havi törlesztő összeg, a B oszlopban pedig az adósság alakulása az egyes törlesztések befizetése után. Az adósság változását a C4...F15 mezők helyén grafikonon is ábrázoljuk. Az első sor és oszlop mezőiben álljon magyarázat, hogy az alattuk, illetve melletük levő mező mit tartalmaz.

Példa:

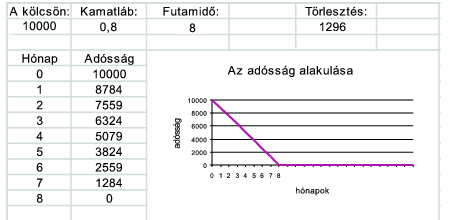
Beküldendő a táblázat (i120.sxc, i120.xls, ...). Feltételezhetjük, hogy n értéke legalább 3 és legfeljebb 24. A táblázat a kamatmentes kölcsönöket (amikor p=0) is kezelje helyesen.

(10 pont)

megoldás, statisztika

S-jelű feladatok A beküldési határidő 2006. január 16-án LEJÁRT.

S. 13. Két játékos egy bábuval felváltva lépked egy irányított gráf csúcsain. Aki nem tud lépni, mert az aktuális helyről nem indul ki él, veszít, és az ellenfél nyer. Ha a bábu harmadszor kerül ugyanarra a mezőre, a játék eredménye döntetlen. Írjunk programot, ami a gráf mindegyik csúcsáról eldönti, hogy onnan indulva mi a legjobb eredmény, amit a kezdő biztosan el tud érni.

A programot a parancssorból fogjuk futtatni két paraméterrel, amelyek az input, illetve output fájl nevét tartalmazzák. Az input fájl fogja tartalmazni a gráfot. Az output fájlban kell felsorolni, hogy az egyes mezők nyerők vagy vesztők.

Az input fájl első sorában a csúcsok és az élek száma (n,m) fog állni. A csúcsokat számozzuk 1-től n-ig. A további m sor egy-egy irányított él kezdő-, illetve végpontjának sorszámát tartalmazza. Az output fájl n sorból álljon; az i-edik sor tartalma legyen N, D vagy V attól függően, hogy az i-edik csúcsból indulva a kezdő játékosnak nyerő stratégiája van, mindkét játékosnak van döntetlen stratégiája, vagy a második játékosnak van nyerő stratégiája.

Feltételezhetjük, hogy a gráfnak legfeljebb csúcsa és legfeljebb éle van.

Példa: a programot az s13 graf.txt eredmeny.txt paranccsal futtatjuk.

Beküldendő a program forráskódja (s13.pas, s13.cpp, ...).

(10 pont)

statisztika