A KöMaL 2006. januári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2006. február 15-én LEJÁRT. |
I. 121. Adott néhány pozitív egész szám: a1,...,ak, és egy s egész szám. Írjunk programot, mely eldönti, hogy az ai számok felhasználásával, pusztán a négy alapművelet és zárójelek segítségével előállítható-e az s szám (minden ai-t pontosan egyszer kell felhasználni). Ha van megoldás, írjunk ki egyet. Ha nincs, akkor írjuk ki azt, hogy ,,Nincs megoldás''.
A program a billentyűzetről (a standard bemenetről) olvassa be az adatokat. Az első sorban k értéke áll, ami legfeljebb 6 lesz. A következő k sor tartalmazza a felhasználható számokat. A (k+2)-edik sor tartalmazza az előírt végeredményt.
Példák:

Beküldendő a program forráskódja (i121.pas, i121.cpp, ...).
(10 pont)
I. 122. Szerkesszük meg ,,plain'' TeX-ben a másodfokú egyenlet megoldóképletének levezetését és a megoldások számának diszkusszióját. A szöveg elején szerepeljen a KöMaL megoldásoknál megszokott fejléc (a feladat száma, név, város, osztály, iskola, e-mail cím). Beküldendő a TeX forrásfájl (i122.tex).
(10 pont)
I. 123. Készítsünk OpenOffice vagy Excel táblázatot, ami legfeljebb hatjegyű egész számokon bemutatja az euklideszi algoritmus működését. A felhasználó az első sor első két mezőjébe írhatja a két pozitív egész számot, amelyek legnagyobb közös osztóját szeretné kiszámítani.
Ezután minden sorba az előző sorbeli két szám közül a kisebbik kerül, illetve a nagyobbik maradéka a kisebbikkel osztva. A sorokat addig folytassuk, amíg meg nem jelenik a számok között a 0. A másik szám a legnagyobb közös osztó, ezt másoljuk az első sor harmadik cellájába.
Példa:
|
Beküldendő a táblázat (i123.sxc, i123.xls).
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2006. február 15-én LEJÁRT. |
S. 14. Egy gyárban egy gép összeszerelését munkafázisokra bontották. Minden munkafázisról tudjuk, hogy hány percig tart, és azt is, hogy elkezdéséhez mely más munkafázisoknak kell befejeződniük. Az olyan munkafázisokat, amelyek nem függnek egymástól, párhuzamosan is végrehajthatjuk.
Tervezzük meg a munkafolyamatot úgy, hogy a kezdéstől a befejezésig a lehető legkevesebb idő teljen el, és adjuk meg, hogy az egyes munkafázisok hányadik percben kezdődjenek.
Bemenet: A munkafázisokat pozitív egész számokkal kódoljuk. Az első sorban a munkafázisok száma áll. Utána soronként egy-egy munkafázis kódja, a hossza (pozitív egész szám), azoknak a fázisoknak a száma, amiktől függ, majd ezek kódjai, szóközökkel elválasztva.
Kimenet: Az első sorban az összeszerelés teljes időtartama. Utána soronként egy-egy fázis kódja és az elkezdésének időpontja, szóközzel elválasztva.
Példa:
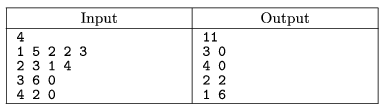
Beküldendő a program forráskódja (s14.pas, s14.cpp, ...).
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

