A KöMaL 2006. februári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2006. március 10-én LEJÁRT. |
K. 73. Az 5 cm oldalhosszúságú ABCD négyzet CD oldalára kifelé megrajzoltuk a CDE szabályos háromszöget.
a) Határozzuk meg az ABE háromszög szögeinek nagyságát.
b) Mekkora a sugara annak a körnek, amelyre az ABE háromszög mindhárom csúcsa illeszkedik?
(6 pont)
K. 74. Az ábrán kétféle festékesdoboz látható. Anna, Balázs, Csilla és Dalma úgy keverik ki a festéket a tojásfestéshez, hogy becsukott szemmel kétszer egymás után belemártják ecsetjüket valamelyik doboz valamelyik rekeszébe, és az így kapott keverékszínt viszik a tojásra. Anna mindkétszer az első, Balázs mindkétszer a második, Csilla először az első, majd a második, Dalma először a második, majd az első dobozba mártja ecsetjét. Melyikük kapja a legkisebb eséllyel a kék és piros keverékeként adódó lila színt?
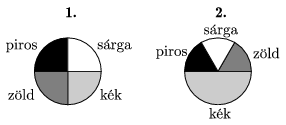
(6 pont)
K. 75. A K1, K2, K3 középpontú r sugarú körök mindegyikére illeszkedik a K pont. Két-két kör további közös pontja a P, Q, illetve R pontok. Mutassuk meg, hogy a K1K2K3 és a PQR háromszögek egybevágók.
(6 pont)
K. 76. Elhelyeztünk 2006 darab, egymást sorban kívülről érintő kis kört egy nagy körben úgy, hogy a kis körök középpontja a nagy kör adott átmérőjére illeszkedik, a kis körök átmérőinek összege pedig a nagy kör átmérőjével egyenlő. Milyen nagyságrendi viszony állapítható meg a kis körök kerületének összege és a nagy kör kerülete között?
(6 pont)
K. 77. A Kelekótya család vett egy falra szerelhető testmagasságmérő szalagot, melynek egyik végén ,,80 cm'', a másik végén ,,180 cm'' jelzés van, mintha a padlón álló 80 és 180 cm közti magasságú emberek lennének vele megmérhetők. A mérőt függőleges helyzetben rögzítették a falra, de az alja nem a megfelelő magasságba került. Utólag még az is kiderült, hogy bár a feltüntetett osztások egyforma távolságban követik egymást, a skála nem centiméterenkénti beosztással készült. Így a padlón állva a 130 cm magas Peti a 120-as jelig ért, míg 150 cm magas nővére a 145-ösig. Legfeljebb hány cm magas embert lehet megmérni ezzel a rosszul skálázott, rosszul felrakott mérőszalaggal?
(6 pont)
K. 78. Ha egy téglatest összes éle mérőszámának összegéből levonjuk a felszínének mérőszámát, majd a kapott számhoz hozzáadjuk a téglatest térfogatának mérőszámát, 8-at kapunk. Bizonyítsuk be, hogy a téglatest egyik élének mérőszáma 2.
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2006. március 16-án LEJÁRT. |
C. 840. 10 darab bankjegy összértéke 5000 Ft. Milyen bankjegyekből állhat ez az összeg?
(5 pont)
C. 841. Pali, a postás egy hosszú utcában először a páratlan oldalon oda-, majd a páros oldalon visszafelé kézbesítette a leveleket. Odafelé harmadannyi ideig állt a postaládák előtt, mint amennyit visszafelé haladt. Visszafelé negyedannyi ideig állt, mint amennyi ideig odafelé haladt. Végül kiderült, hogy ugyanannyi ideig tartott mindkét oldalon a kézbesítés. Hogyan aránylik egymáshoz az út (állás nélküli) haladási átlagsebessége oda és a vissza?
(5 pont)
C. 842. Tíznél több egységnyi fakockából egy nagy, tömör kockát építettünk, majd a nagy kocka minden lapját befestettük. Ezután különválasztottuk a többitől azokat a kis kockákat, amelyeknek van befestett lapja. Lehet-e a festett kockák száma többszöröse a festetlen kockák számának?
(5 pont)
C. 843. Az ABC háromszögben . Az AC oldal A-hoz közelebbi harmadolópontját jelölje P. Tudjuk, hogy
. Mekkora az
?
(5 pont)
C. 844. Egy henger tengelymetszetének kerülete 90 cm. Legfeljebb mekkora lehet a henger térfogata?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2006. március 16-án LEJÁRT. |
B. 3882. Az ABC háromszög oldalaira kifelé megrajzoltuk a BAD és ACE szabályos háromszögeket. Igazoljuk, hogy a BE egyenesnek a CD egyenesre való tükörképe átmegy az A ponton.
(3 pont)
B. 3883. Igazoljuk, hogy ha az a, b egész számok különbsége osztható 100-zal, akkor a100-b100 osztható 10 000-rel.
(3 pont)
B. 3884. Három egységnyi sugarú kör mindegyike átmegy a P ponton, további metszéspontjaik pedig A, B és C. Mekkora az ABC háromszög köré írható kör sugara?
(4 pont)
B. 3885. Egy háromszög beírt körének sugara r, körülírt körének sugara R, egyik szöge pedig  . Tegyük fel, hogy
. Tegyük fel, hogy
Mutassuk meg, hogy a háromszög egyenlő szárú.
(4 pont)
B. 3886. Az ABCD húrnégyszög átlói merőlegesek egymásra. Milyen arányban osztja az átlók metszéspontjából az AB egyenesre állított merőleges a CD oldalt?
(4 pont)
B. 3887. Tíznél több egységnyi fakockából egy nagy, tömör kockát építettünk, majd a nagy kocka minden lapját befestettük. Ezután különválasztottuk a többitől azokat a kis kockákat, amelyeknek egyetlen lapja sincs befestve. Lehet-e ezen kockák száma többszöröse a többi kocka számának?
(4 pont)
B. 3888. Mely m>1 egészekre létezik az számoknak olyan
sorrendje, hogy az
összegek mind különböző maradékot adnak m-mel osztva?
(5 pont)
B. 3889. Egy bűvésztől láttam a következő mutatványt. Egy néző véletlenszerűen kiválasztott 5 lapot az 52 lapos francia kártyából, és átadta őket a bűvész segédjének. (A segéd a bűvész állandó partnere volt, így korábban már megállapodhattak.) A segéd megnézte az 5 lapot, és a bűvésznek egyesével átadott közülük 4-et. Ezután a bűvész -- anélkül, hogy bármi egyéb információt kapott volna -- megnevezte az ötödik lapot.
A mutatvány végeztével a bűvész az alábbi módon próbálta meggyőzni a matematika iránt érdeklődő nézőket:
,,A segítőm négy kártyát mutatott nekem, és ez a négy kártya tetszőlegesen kerülhet ki a pakliból. Információt tehát kizárólag a kártyák bemutatásának a sorrendjén keresztül közölhetett velem. Mint ismeretes, 4 kártyát 4!=24-féleképpen lehet sorbarendezni, az ötödik lap azonban 52-4=48-féle lehetett. Éppen 1 bit információ hiányzik tehát, ennek a pótlásához kell a csoda.''
Igaz-e, hogy a mutatványhoz valóban természetfölötti képességekre van szükség?
Javasolta: Gáspár Merse Előd, fizikus
(5 pont)
B. 3890. Egy nemzetközi konferencián 200 tudós vesz részt. Mindegyikük legfeljebb 4 nyelven beszél, továbbá bármely három között van kettő, akik beszélnek közös nyelven. Bizonyítsuk be, hogy van olyan nyelv, amit közülük legalább 26-an beszélnek.
(4 pont)
B. 3891. Tegyük fel, hogy x és y racionális számok, amelyekre x5+y5=2x2y2. Bizonyítsuk be, hogy 1-xy egy racionális szám négyzete.
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2006. március 16-án LEJÁRT. |
A. 392. Egy tetraéder beírt gömbjének sugara r. Három olyan gömb létezik, ami a tetraéder lapsíkjait érinti úgy, hogy egyik érintési pont sincs a tetraéder felületén; ezek sugara r1, r2, illetve r3. Mutassuk meg, hogy
r1+r2+r3>9r.
(5 pont)
A. 393. Igazoljuk, hogy ha n>1 egész szám, és 3n+4n osztható n-nel, akkor n osztható 7-tel.
(5 pont)
A. 394. Bizonyítsuk be, hogy ha a1,a2,...,aN nemnegatív valós számok, és nem mindegyikük 0, akkor létezik olyan k pozitív egész szám, és léteznek olyan egészek, amelyekre
A 2005. évi Kürschák-verseny 1. feladata nyomán
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

