KöMaL Problems in Mathematics, October 2006
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on November 10, 2006. |
K. 91. 2163 is a four-digit number in which the digit in the units' place is three times the digit in the hundreds' place, and the digit in the tens' place is two times the sum of the digits in the hundreds' place and the thousands' place. Is it true that such four-digit numbers are all divisible by 3?
(6 pont)
solution (in Hungarian), statistics
K. 92. Pilots use the face of a clock to express bearings. The actual flight direction is identified with 12 o'clock, so, for example, instead of ``90 degrees to the right'' they say ``3 o'clock'', or ``behind me'' equals to ``6 o'clock''. Follow the flight path of a reconnaissance plane that takes off from the base and flies 3 minutes in a given direction, then turns to 2 o'clock and flies 4 minutes, then turns again to 2 o'clock and flies 3 minutes, finally the plane turns to 4 o'clock and flies 9 minutes. In what clock direction should the plane be turned to in order to fly straight back to the base? How many minutes does this take?
(6 pont)
solution (in Hungarian), statistics
K. 93. Sherlock Holmes was investigating a crime in the Musgrave property famous for a beautiful elm tree. Looking for the hidden treasure, he was to ``walk ten and ten steps to the north, five and five steps to the east, two and two steps to the south, and one and one step to the west.'' Holmes found out, however, that one of the directions was wrong, one should walk in the opposite direction instead (for example, south instead of north). Since he did not know which was wrong, he tried all possibilities. Each walk ended within the park of the Musgraves. Given that Holmes' steps are 80 cm long and the park is a rectangle with sides in the north-south and east-west directions, find the minimum possible area of the park.
(6 pont)
solution (in Hungarian), statistics
K. 94. When the five-digit number is multiplied by 4, the five-digit number
is obtained. Find the value of
. (A, B, C, D, E denote different digits.)
(6 pont)
solution (in Hungarian), statistics
K. 95. A one-digit number is written in each field of a 3×3 chessboard. A chessman is moved in an L-shaped path from one field to another (the way that a knight moves). Such an L consists of four fields. In how many different ways is it possible to fill out the 3×3 table with (not necessarily different) one-digit numbers so that the sum of the four numbers in every such L-shaped move is the same?
(6 pont)
solution (in Hungarian), statistics
K. 96. The sides of an equilateral triangle ABC are 16 cm long. The side AC is extended beyond A by one quarter of the length AC and the point P is obtained. The point P is connected by a line to the point dividing the side AB in a 1:3 ratio (so that the shorter segment of AB lies next to A.) This line divides the side BC into two pieces. Find their lengths.
(6 pont)
 |
Problems with sign 'C'Deadline expired on November 15, 2006. |
C. 865. Which number has the form 503 in base n and 305 in base (n+2)?
(5 pont)
solution (in Hungarian), statistics
C. 866. Find the value of parameter a such that the distance between two roots of the equation x2-4ax+5a2-6a=0 is the greatest.
(5 pont)
solution (in Hungarian), statistics
C. 867. Starting from the origin in the usual Cartesian coordinate system, a broken line segment is drawn. We arrive back at the y-axis in every fourth step, see the figure.
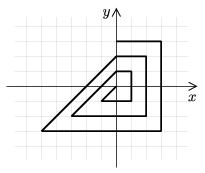
Using a certain ball-pen and a coordinate system with unit length of 0.5 cm, we draw broken line segments of length 8000 meters as in the figure. Count how many times we arrive back at the y-axis.
(5 pont)
solution (in Hungarian), statistics
C. 868. Four distinct points are given in the plane. The pairwise distance between 4 points is 1, and the distance between a certain pair is 1.2. What can be said about the distance between the remaining 2 points?
(5 pont)
solution (in Hungarian), statistics
C. 869. A cylinder of height is inscribed into a sphere of radius R. Determine the ratio of their volumes.
(5 pont)
 |
Problems with sign 'B'Deadline expired on November 15, 2006. |
B. 3932. Find all positive prime numbers that satisfy equation x2+y2=z-16.
(3 pont)
solution (in Hungarian), statistics
B. 3933. A sequence an is defined as a1=1, a2n=an, a2n+1+an=1. Determine the value of a2006.
(3 pont)
solution (in Hungarian), statistics
B. 3934. A rectangle and two squares are drawn inside a right-angled triangle shown in the figure. Prove that the height of the rectangle is equal to the sum of heights of the squares.
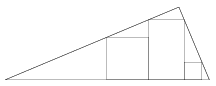
(3 pont)
solution (in Hungarian), statistics
B. 3935. Some characters in a Hamlet play are paired, for example, both members of a pair can play the role of Gertrude and the role of Player Queen. Before every performance it is decided by a lot who will play Gertrude and who Player Queen. Other pairs are also chosen by a similar lot. Sarah has already seen Hamlet, but she wants to see it again with a different actor playing the other member of the pair Gertrude/Player Queen, Claudius/Player King and Ophelia/Fortinbras, although not necessarily in one performance. How many tickets should she still buy to see all three roles in the other casting with 90% probability?
(4 pont)
solution (in Hungarian), statistics
B. 3936. Determine the conditions on the real numbers a, b and c such that for every positive integer n there exists a triangle with side lengths an, bn and cn.
Suggested by Ervin Fried, Budapest
(4 pont)
solution (in Hungarian), statistics
B. 3937. A triangle is made by soldering three thin metal rods of length 8, 15 and 17 cm together. A solid ball of radius 5 cm is put on this triangle frame held horizontally. In what ratio does the plane of the triangle divide the volume of the ball?
(4 pont)
solution (in Hungarian), statistics
B. 3938. The sum of integers all greater than 1 is 2006. What is the minimal value of
?
(4 pont)
solution (in Hungarian), statistics
B. 3939. Find the angle encompassed by the hypotenuse of a right-angled triangle with circumference of 2 units, as seen from a point lying on the inner angle bisector of the right angle at a distance of from that vertex.
(4 pont)
solution (in Hungarian), statistics
B. 3940. Let a, o and c be three lines in the plane. Consider all squares ABCD such that vertex A lies on line a, the opposite vertex C on line c, and the centre of the square O lies on line o. Find the locus of vertices B and D.
Suggested by M. Danka and B. Kalló, 9th-grade students of Fazekas Mihály Gimnázium, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 3941. Find all positive rational triples (p;q;r) such that p+q+r, and pqr are all integers.
(5 pont)
 |
Problems with sign 'A'Deadline expired on November 15, 2006. |
A. 407. In pyramid ABCDE, the angle between plane ACE and faces ABCD, ABE, BCE, CDE and DAE are all 45o. Prove that AB2+AD2=BC2+CD2.
(5 pont)
A. 408. The positive reals and b1
 b2
b2 ...
... bn satisfy a1+a2+...+ak
bn satisfy a1+a2+...+ak b1+b2+...+bk for all 1
b1+b2+...+bk for all 1 k
k n. Prove that
n. Prove that
(5 pont)
A. 409. For a positive integer m, let s(m) be the sum of the digits of m. For n 2, let f(n) be the minimal k for which there exists a set S of n positive integers such that
2, let f(n) be the minimal k for which there exists a set S of n positive integers such that for any nonempty subset X
 S. Prove that there are constants 0<C1<C2 with C1log10n
S. Prove that there are constants 0<C1<C2 with C1log10n f(n)
f(n) C2log10n.
C2log10n.
U.S.A. Mathematical Olympiad, 2005
(5 pont)
Upload your solutions above.
