A KöMaL 2006. októberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2006. november 10-én LEJÁRT. |
K. 91. A 2163 olyan négyjegyű szám, amelyben az egyesek helyén álló számjegy háromszorosa a százas helyiértéken álló számjegynek, a tízes helyiértéken álló számjegy pedig kétszerese a százas és az ezres helyiértéken álló számjegyek összegének. Igaz-e, hogy az ilyen tulajdonságú négyjegyű számok mindegyike osztható 3-mal?
(6 pont)
K. 92. A pilóták a mutatós óra számlapjának segítségével határozzák meg repülési irányukat. A pilóta mindenkori repülési iránya esik a 12 óra irányába, így a ,,jobbra 90 fok'' helyett ,,3 óra irányában''-t mondanak, a ,,mögöttem'' helyett ,,6 óra irányában''-t. Kövessük egy felderítő repülő útját, amely a támaszpontról indulva egy adott irányba repül 3 percig, majd 2 óra irányába kanyarodik és repül egyenesen 4 percig, aztán újra 2 óra irányába kanyarodik és repül egyenesen 3 percig, végül 4 óra irányába kanyarodik és repül egyenesen 9 percig. Hány óra irányába kell kanyarodnia, hogy egyenesen a támaszpontra tudjon utána repülni? Hány perces repüléssel ér vissza a támaszpontra ebben az irányban haladva?
(6 pont)
K. 93. Sherlock Holmes egy alkalommal a szilfájáról híres Musgrave birtokon nyomozott. A szilfa csúcsának árnyékától kellett ,,északnak tízet és tízet, keletnek ötöt és ötöt, délnek kettőt és kettőt, nyugatnak egyet és egyet'' lépnie, hogy a rejtekhely nyomára bukkanjon. Holmes tudomására jutott azonban, hogy a szövegben szereplő egyik égtáj helyett pont az ellenkező felé (pl. észak helyett dél) kellett volna lépnie. Mivel azonban nem tudta, melyik helyett, az összes lehetőséget kipróbálta, és mindegyik a birtok angolparkján belüli helyen végződött. Tudjuk, hogy Holmes egy lépése 80 cm, és az angolpark alaprajza észak--dél--kelet--nyugat tájolású téglalap. Legalább mekkora az angolpark területe?
(6 pont)
K. 94. Az ötjegyű számot 4-gyel szorozva az ötjegyű
számot kapjuk. Határozzuk meg
értékét. (A, B, C, D, E különböző számjegyeket jelölnek.)
(6 pont)
K. 95. A 3×3-as sakktábla mezőibe úgy írtunk egy-egy számjegyet, hogy bármely mezőről L-alakban (ahogyan a huszár lép) csúsztatva a bábut a négy érintett mezőn levő szám összege mindig ugyanaz az érték. Hányféleképpen tölthető ki ilyen módon a sakktábla, ha minden mezőre írtunk egy, a többitől nem feltétlenül különböző számjegyet?
(6 pont)
K. 96. A 16 cm oldalhosszúságú ABC szabályos háromszög AC oldalát meghosszabbítottuk az A-n túl az AC oldal negyedével és így a P pontot kaptuk. A P pontot kössük össze az AB oldal A-hoz közelebbi negyedelő pontjával. Az így kapott egyenes mekkora részekre vágja a BC oldalt?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2006. november 15-én LEJÁRT. |
C. 865. Melyik az a szám, amelynek az n-alapú számrendszerben felírt alakja 503, az (n+2)-alapú számrendszerben pedig 305?
(5 pont)
C. 866. Az a paraméter mely értékére lesz az x2-4ax+5a2-6a=0 másodfokú egyenlet két gyöke a legmesszebbre egymástól?
(5 pont)
C. 867. A derékszögű koordinátarendszer origójából indulva rajzolunk egy töröttvonalat az ábra szerint. Minden negyedik szakasz megrajzolása után visszajutunk az y tengelyhez, ahogyan az ábra mutatja.
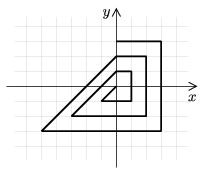
Egy hazánkban gyártott golyóstoll csomagolásáról megtudtuk, hogy az íráshossza 8000 méter. Ha ezzel a tollal megrajzolnánk egy 0,5 cm egységű koordinátarendszerben a megadott 8000 méter hosszúságú vonalat, hányszor érkeznénk vissza az y tengelyhez?
(5 pont)
C. 868. Adott a síkban négy különböző pont. A négy pont közötti hat távolság közül négy távolság egységnyi, egy pedig 1,2. Mekkora lehet az ismeretlen hatodik távolság?
(5 pont)
C. 869. Egy R sugarú gömbbe írt henger magassága . Hányadrésze a henger térfogata a gömb térfogatának?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2006. november 15-én LEJÁRT. |
B. 3932. Oldjuk meg az x2+y2=z-16 egyenletet a pozitív prímszámok halmazán.
(3 pont)
B. 3933. Az an sorozatot a következőképpen értelmezzük: a1=1, a2n=an, a2n+1+an=1. Mennyi a2006?
(3 pont)
B. 3934. Egy derékszögű háromszögbe az ábra szerint egy téglalapot és két négyzetet írtunk. Mutassuk meg, hogy a téglalap magassága a négyzetek magasságának az összege.
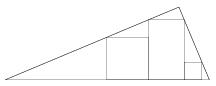
(3 pont)
B. 3935. Egy Hamlet előadáson több szerep párosítva van, például Gertrudis és a Színészkirálynő szerepét ketten is tudják. Az előadás előtt sorsolással döntik el, hogy kettejük közül ki játssza aznap a Színészkirálynőt, illetve Gertrudist. Hasonló sorsolással döntenek a további párok esetében is. Sári egyszer már látta az előadást, de a Gertrudis/Színészkirálynő, Claudius/Színészkirály, Ophelia/Fortinbras szerepeket a másik változatban is szeretné megnézni, bár nem feltétlenül egy előadáson. Hány előadásra váltson még jegyet, hogy legalább 90% legyen annak a valószínűsége, hogy mindhárom szerepet látja a másik szereposztásban is?
(4 pont)
B. 3936. Milyen feltételeknek kell teljesülni az a, b, c valós számokra ahhoz, hogy minden n természetes számra létezzék olyan háromszög, amelynek az oldalai an, bn és cn?
Javasolta: Fried Ervin (Budapest)
(4 pont)
B. 3937. Három vékony fémpálcából 8, 15, 17 cm oldalú háromszöget forrasztottunk, és a vízszintesen tartott háromszög vázra egy 5 cm sugarú tömör gömböt helyeztünk. Milyen arányban osztja a háromszög síkja a gömb térfogatát?
(4 pont)
B. 3938. Az 1-nél nagyobb egészek összege 2006. Mekkora az
összeg lehetséges legkisebb értéke?
(4 pont)
B. 3939. Mekkora szög alatt látszik egy 2 egységnyi kerületű derékszögű háromszög átfogója a derékszög belső szögfelezőjének félegyenesén a csúcstól távolságra lévő pontból?
(4 pont)
B. 3940. Adott három egyenes a síkon: a, o és c. Tekintsük azokat az ABCD négyzeteket, amelyeknek A csúcsa az a egyenesre, a vele szemközti C csúcs a c egyenesre, míg a négyzet O középpontja az o egyenesre illeszkedik. Határozzuk meg a B és D csúcsok mértani helyét.
Javasolta: Danka Miklós és Kalló Bernát (Fazekas Mihály Főv. Gyak. Gimn., 9. évf.)
(5 pont)
B. 3941. Határozzuk meg az összes olyan (p;q;r) pozitív racionális számokból álló hármast, amelyre p+q+r, , pqr mindegyike egész szám.
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2006. november 15-én LEJÁRT. |
A. 407. Az ABCDE négyoldalú gúlában az ACE sík 45o-os szöget zár be az ABCD, ABE, BCE, CDE és DAE lapok mindegyikével. Igazoljuk, hogy AB2+AD2=BC2+CD2.
(5 pont)
A. 408. Az és
pozitív valós számokra teljesül, hogy tetszőleges 1
 k
k n esetén
n esetén . Bizonyítsuk be, hogy
(5 pont)
A. 409. Tetszőleges pozitív egész m-re legyen s(m) az m számjegyeinek összege. Tetszőleges n 2-re legyen f(n) a legkisebb k, amihez létezik olyan n-elemű, pozitív egészekből álló S halmaz, amelyre
2-re legyen f(n) a legkisebb k, amihez létezik olyan n-elemű, pozitív egészekből álló S halmaz, amelyre bármely nemüres X
 S esetén. Bizonyítsuk be, hogy léteznek olyan 0<C1<C2 valós számok, amelyekre
S esetén. Bizonyítsuk be, hogy léteznek olyan 0<C1<C2 valós számok, amelyekre
C1log10n f(n)
f(n) C2log10n.
C2log10n.
U.S.A. Matematikai Olimpia, 2005
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

