KöMaL Problems in Mathematics, November 2006
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on December 11, 2006. |
K. 97. There are 7 houses in Dragon Street, numbered 1 to 7. Last week, Mr. D. E. Livery the postman delivered letters to two houses every day. There are two houses where he did not brought anything during the whole week, but he visited all the other houses twice. The sum of the number of the houses visited by Mr. Livery was 5 on Monday, 8 on Tuesday, 9 on Wednesday, 13 on Thursday and 7 on Friday. (There is no mail on Saturday and Sunday.) Which are the two houses that did not receive any letter last week?
(6 pont)
solution (in Hungarian), statistics
K. 98. In a certain year, the 1st of January was not a weekend day but the 31st of December was. The school year started on the 1st of September. Which day of the week was that?
(6 pont)
solution (in Hungarian), statistics
K. 99. There are three kind of candies packed in a box, 16 of them altogether. The diagram shows the arrangement of the candies. The total mass of the four ones in the first row is 14 dkg; that of them in the second row is 11 dkg; finally, the total mass of the candies in the first column is 10 dkg. How much is the total mass of the candies in the whole box?
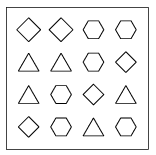
(6 pont)
solution (in Hungarian), statistics
K. 100. Solve the following equation on the set of real numbers: .
(6 pont)
solution (in Hungarian), statistics
K. 101. George is 17 years older than Anna. If George's age in years is written after Anna's age, a four-digit square number is obtained. The same will be true in 13 years' time. How old are they now?
(6 pont)
solution (in Hungarian), statistics
K. 102. Four cardboard discs, two of 32 dm2 and two of 21 dm2 are placed on a tabletop of 1 m2. None of them overhang the edge of the table. Is it true that there are two discs that overlap on an area of at least 4 dm2?
(6 pont)
 |
Problems with sign 'C'Deadline expired on December 15, 2006. |
C. 870. A car dealer sold 7 cars per day on the average in a certain period. If the day of the smallest number of cars sold is not counted, the average number of cars sold per day will be 8. If the day of the largest number of cars sold is not counted, the average will be 5. Finally, if both of these days are ignored them, the average will be 5.75 cars per day. What was the total number of cars sold by the dealer in the given period?
(5 pont)
solution (in Hungarian), statistics
C. 871. Prove that if the expression
is well defined, then its value is independent of the values of the variables x, y and z.
(5 pont)
solution (in Hungarian), statistics
C. 872. Consider a quadrant of a disc of radius 12 cm. A semicircle is drawn over one of the radii bounding the quadrant, and cut out of it. What is the radius of the largest possible circle that can be inscribed in the remaining figure?
(5 pont)
solution (in Hungarian), statistics
C. 873. For what real values of x will the value of the expression be a maximum?
(5 pont)
solution (in Hungarian), statistics
C. 874. The roof of a newsstand with a square base 3 m on a side consists of two regular triangular prisms that intersect each other. One lateral face of each prism coincides with the ceiling of the newsstand. (The prisms are rotated through 90o relative to each other.) Calculate the surface area of the roof.
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 15, 2007. |
B. 3942. Find all two-digit even numbers , whose fifth powers end in
.
(Mathematics competition for teacher training colleges, 1973).
(3 pont)
solution (in Hungarian), statistics
B. 3943. The diagonals of the trapezium ABCD intersect at the point M. The areas of the triangles ABM and CDM are 18 and 50 units, respectively. Find the area of the trapezium.
(3 pont)
solution (in Hungarian), statistics
B. 3944. Sketch in the cartesian plane the region consisting of the points (x,y) such that .
(3 pont)
solution (in Hungarian), statistics
B. 3945. Solve the following simultaneous equations: x3+y3+z3=8, x2+y2+z2=22, .
(3 pont)
solution (in Hungarian), statistics
B. 3946. The angle bisector drawn from vertex C of an acute angled triangle ABC intersects the opposite side at the point F. The feet of the perpendiculars drawn from the point F to the sides BC and CA are P and Q, respectively. Let M denote the intersection of the lines AP and BQ. Prove that AB and CM are perpendicular to each other.
(4 pont)
solution (in Hungarian), statistics
B. 3947. Let h denote the length of the tangents drawn to a circle from an exterior point P, and let the midpoint of the line segment connecting the points of contact be F. Prove that a chord AB of the circle satisfies the equality AP.PB=h2 if and only if the line AB passes through the point P or the point F.
(4 pont)
solution (in Hungarian), statistics
B. 3948. a and b are real numbers, such that a2+4b2=4. What is the largest possible value of 3a5b-40a3b3+48ab5?
(Suggested by Z. Horváth, Veresegyház)
(4 pont)
solution (in Hungarian), statistics
B. 3949. For what values of the positive integer n is there a simple graph in which the degree of each vertex is at most n, and there are i vertices of degree i for all 1 i
i n?
n?
(Suggested by G. Mészáros, Kemence)
(4 pont)
solution (in Hungarian), statistics
B. 3950. Let H be the set of integers not greater than 2006: H={1,2,...,2006}. Let D denote the number of those subsets of the set H in which the number of elements divided by 32 leaves a remainder of 7, and let S denote the number of those subsets of the set H in which the number of elements divided by 16 leaves a remainder of 14. Prove that S=2D.
(Based on an OKTV (National Competition) problem)
(5 pont)
solution (in Hungarian), statistics
B. 3951. Let a, b, n, k be positive integers, such that n is odd, p is an odd prime number, and an+bn=pk. Prove that n is a power of p with a non-negative integer exponent.
(5 pont)
 |
Problems with sign 'A'Deadline expired on December 15, 2006. |
A. 410. The angle bisectors of triangle ABC intersect sides BC, CA and AB at points A1, B1 and C1, respectively. On line A1B1, denote by F the perpendicular foot point of C1. Prove that line FC1 bisects angle AFB.
(5 pont)
A. 411. Let be positive real numbers satisfying
. Prove that
.
(Vietnamese competition problem)
(5 pont)
A. 412. Let t be an irrational number and let
for all integers x, y. The function f(x,y) has many decompositions of the form f(x,y)=u(x)+v(y)+w(x-y), where the functions u, v and w map the set of integers to the set of reals. Prove that (a) There exists a case when u, v and w are bounded; (b) There exists a case when u, v and w attain only integers; (c) There exists no case when u, v and w are bounded and attain only integers.
(Proposed by Tamás Keleti, Budapest)
(5 pont)
Upload your solutions above.
