KöMaL Problems in Mathematics, December 2006
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on January 10, 2007. |
K. 103. Andrew, Bill, Charlie and Dennis are playing cards. In each game, only three of the four boys are playing. They get points from one another, depending on the outcome of the game: either one player gets points from the other two or two players get points from the third one. (If there are two losers or two winners then they do not necessarily lose or gain the same number of points.) At the beginning, everyone had 100 points. The boys have played four games, each time leaving out a different person. The points that each participant had during the card play are tabulated on the diagram. Which player was left out from the respective games?
|
(6 pont)
solution (in Hungarian), statistics
K. 104. We have a large supply of boxes: each of them is either small, or medium or large. 11 large boxes were put on the table. Some were left empty and 8 medium boxes were put in each of the rest of them. Some of the medium boxes were also left empty, and 8 small boxes (all empty) were put in each of the remaining ones. Thus there were 102 empty boxes on the table. How many boxes are there on the table altogether? (Boxes of the same size cannot be put into each other.)
(6 pont)
solution (in Hungarian), statistics
K. 105. A book contains 700 psalms, numbered from 1 to 700. The congregation sings one of them every Sunday. The number of the chosen psalm is displayed as a 3-digit number on a special counter, fabricated from three small wooden cubes. (One or two-digit numbers are displayed with leading zeros, e.g. 3 appears as 003 and 28 as 028.) The is one digit on faces of the cubes, respectively, and 6 can also be interpreted as a 9. a) How many cubes are needed to display every possible number? How the digits are arranged on the faces? b) How many more psalms can be included in the book without adding further cubes?
(6 pont)
solution (in Hungarian), statistics
K. 106. The sum of the squares of three consecutive odd natural numbers is a four-digit number of identical digits. Find all possible sets of three such numbers. Are there five consecutive odd natural numbers, such that the sum of their squares is a six-digit number of equal digits?
(6 pont)
solution (in Hungarian), statistics
K. 107. If two digits of the four-digit number 1234 are cancelled in every possible way and the remaining digits are read as a two-digit number, the numbers 12, 13, 14, 23, 24, 34 are obtained. Their sum is 120. Find a four-digit number for which this sum is a) 540; b) 220.
(6 pont)
solution (in Hungarian), statistics
K. 108. A square patch of grass, 100 m on a side is surrounded by a paved road along its boundary. Most people want to get from corner A of the square to the midpoint F of an opposite side. They walk along the path ABF, but some of them have started a path through the grassy area. They walk along the side AB for a while, then they are heading towards F along a straight line through the grass, as shown in the diagram. Thus they walk 25% less compared to the path along the border. How far is the turning point K of the path from the point A?
(6 pont)
 |
Problems with sign 'C'Deadline expired on January 15, 2007. |
C. 875. There are two kind of rolls sold in Hungary, their prices are 15 forints and 12 forints, respectively. (Forint is the Hungarian currency, HUF.) We buy some of each. a) Is it possible that we pay 500 forints? b) Is it possible that we pay 600 forints?
(5 pont)
solution (in Hungarian), statistics
C. 876. Solve the following simultaneous equations:
x+y=x2+2xy+y2,
x-y=x2-2xy+y2.
(5 pont)
solution (in Hungarian), statistics
C. 877. When a rectangular sheet of paper is folded along a diagonal, the vertices form a cyclic trapezium with three equal sides, and the length of the fourth side is . Find the dimensions of the rectangle?
(5 pont)
solution (in Hungarian), statistics
C. 878. A cube is inscribed in a regular four-sided pyramid whose height is the double of the length of the sides of its base. What proportion of the volume of the pyramid is occupied by this cube. (The inscribed cube has four vertices on the lateral edges and the other four are lying on the base of the pyramid.)
(5 pont)
solution (in Hungarian), statistics
C. 879. I go shopping with 5000 forints. (Forint is the Hungarian currency, HUF.) I drop in three shops, and I find some gift in each of them that I like and buy it if I have enough money. The price of each gift is one of 1000, 1500 or 2000 forints with probability 1/3, independently in each shop. What is the probability that I will end up with three presents and even with some money left?
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 15, 2007. |
B. 3952. Santa Claus is putting Christmas candies in small bags. If he puts 35 candies in each bag, there will be 7 candies left. What can be the overleft if he puts only 15 candies in each bag?
(3 pont)
solution (in Hungarian), statistics
B. 3953. Given are 100 real numbers whose sum is equal to zero. At least how many pairs can be chosen from them such that the sum of the numbers in each pair is not negative?
(5 pont)
solution (in Hungarian), statistics
B. 3954. Solve the following simultaneous equations:
(Source: Hungarian Mathematics Competitions Across the Border, by Gy. Oláh)
(4 pont)
solution (in Hungarian), statistics
B. 3955. In a theatre performance of Hamlet, Acts 2 to 5 are played in a part of the auditorium chosen at random by means of a draw. The stalls are divided into four sectors. The part of the audience with seats in the sector selected will move to another sector, taking also their chairs with them. Provided that each of the four sectors are large enough (that is, if one chooses a sector, then there will always be enough space for one's chair there) and assuming that each sector is equally likely to be chosen, what is the proportion between the probabilities that one needs to move twice during the play or only once?
(4 pont)
solution (in Hungarian), statistics
B. 3956. 2006 points are given on the plane. At most how many of them forms acute-angled triangles, respectively, with every pair chosen from the remaining 2005 points?
(4 pont)
solution (in Hungarian), statistics
B. 3957. D is an interior point of the side AB of a triangle ABC. The inscribed circle of the triangle ABC touches the side AB at the point P. The inscribed circles of the triangles ADC and DBC are touching the side DC at Q and R, respectively. Show that DP=QR.
(3 pont)
solution (in Hungarian), statistics
B. 3958. The triangle ABC is right angled at C and its incentre is O. The perpendiculars drawn at the point O to the line segments OA and OB meet the side AB at P and Q, respectively. The foot of the perpendicular from P to the side BC is P', and that from Q to the side AC is Q'. Prove that the points P', Q' and O are collinear.
(4 pont)
solution (in Hungarian), statistics
B. 3959. Let K be an arbitrary point inside the triangle A1A2A3 and denote the centroid of the triangle KAjAkAs by Si (i=1,2,3,). Prove that the line segments AiSi are concurrent.
(4 pont)
solution (in Hungarian), statistics
B. 3960. Draw perpendiculars to the real axis of a hyperbola at its endpoints. Let P and Q denote the intersections of these perpendiculars with an arbitrary tangent to the curve, respectively. Prove that the line segment PQ subtends right angles at the foci.
(Suggested by I. Vajda, Budapest)
(5 pont)
solution (in Hungarian), statistics
B. 3961. Let a and b denote positive integers, such that an+n divides bn+n for all positive integers n. Prove that a=b.
(5 pont)
 |
Problems with sign 'A'Deadline expired on January 15, 2007. |
A. 413. Let O be the point of intersection of the diagonals AC, BD of a convex quadrilateral ABCD. Let G1 and G2 be the centroids of triangles OAB and OCD, respectively. Let H1 and H2 be the orthocenters of triangles OBC and ODA, respectively. Prove that G1G2 is perpendicular to H1H2.
(Vietnamese competitoon problem)
(5 pont)
A. 414. Prove
for all positive reals x, y, z.
(Iranian competition problem)
(5 pont)
A. 415. Let a>b and n be arbitrary positive integers. Prove that n divides 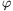 (an-bn).
(an-bn).
(Proposed by Balázs Strenner, Budapest)
(5 pont)
Upload your solutions above.
