KöMaL Problems in Mathematics, January 2007
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on February 15, 2007. |
K. 109. In a football championship, Peter's favourite team scored a total of three goals in the first four matches played. Other teams scored a total of two goals against the team. Given that a team gets 3 points for winning, 1 for a draw and none if they lose the game, how many points may Peter's favourite team have after the four matches played?
(6 pont)
solution (in Hungarian), statistics
K. 110. In Dragon Castle, 14-headed baby dragon is sleeping while mummy dragon is making pancakes. She lays them on a plate and leaves home. One head wakes up, eats 1/11 of the pancakes and falls asleep again. Then another head wakes up, eats 1/13 of the remaining pancakes and falls asleep again. Next, three heads wake up at the same time, eat 1/14 of the pancakes each, and finally they wake up the rest of the heads, too. Those who have eaten, do not get any more pancakes, the remaining 9 heads eat them all. (They do not necessarily eat the same number.) How many pancakes may have been on the plate, given that every head ate a whole number of pancakes, and if they had shared them equally, no one would have got more than 143?
(6 pont)
solution (in Hungarian), statistics
K. 111. In a game, two dice are rolled and there are 9 cards numbered 1 to 9. The total of the numbers rolled is to be put together as a sum of number cards (or a single card). Each card can only be used once. Used cards are set aside and the sum of the next two numbers rolled is put together out of the remaining cards. And so on while it is possible.
a) What is the minimum number of rolls may in a sequence of rolls where all number cards are used up? Give an example, too.
b) In the worst case, what is the smallest number of rolls that may end the game?
(6 pont)
solution (in Hungarian), statistics
K. 112. In each row of the correct addition below, cancel one digit. Push the remaining digits together so that three-digit numbers are formed. Another digit is cancelled from each row and the remaining numbers are pushed together so that two-digit numbers are formed. Then another digit is cancelled in each row to leave one-digit numbers. The addition remains correct all the way. What were the cancelled digits in each step? Find all possible solutions.
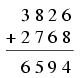
(6 pont)
solution (in Hungarian), statistics
K. 113. How many four-digit numbers are there that consist of different digits, end in 5 and are divisible by each of their digits?
(6 pont)
solution (in Hungarian), statistics
K. 114. Steve has three classmates named Smith, four named Black, one named White and two named Tailor. Among these boys, there are four with the first name of Jack, two called Alex, three called Bob and one Martin. Each boy has only one first name, and no two boys in the class have exactly the same name. What are the full names of these classmates of Steve?
(6 pont)
 |
Problems with sign 'C'Deadline expired on February 15, 2007. |
C. 880. Which six-digit number will be multiplied by three if its first digit is reduced by three and a digit of three is attached to the end?
(5 pont)
solution (in Hungarian), statistics
C. 881. Solve the equation .
(5 pont)
solution (in Hungarian), statistics
C. 882. The legs of a right-angled triangle are a and b. The line segment of length d connecting the vertex of the right angle to a point of the hypotenuse encloses an angle 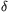 with the leg a. Prove that
with the leg a. Prove that
(5 pont)
solution (in Hungarian), statistics
C. 883. A trough with regular triangular cross section is filled to the brim with water. Through what angle should it be tilted in order to make one fifth of the water flow over? The triangular ends of the trough should move in their vertical planes.
(5 pont)
solution (in Hungarian), statistics
C. 884. A roll of a die is said to be successful if the score is at least three. Which is more probable: Rolling at least once successfully out of two or at least twice out of four?
(5 pont)
 |
Problems with sign 'B'Deadline expired on February 15, 2007. |
B. 3962. In how many different ways can one pay 1000 forints (Hungarian currency, HUF) in 100, 20 and 5-forint coins, exactly 100 of them altogether? (The order does not matter.)
(3 pont)
solution (in Hungarian), statistics
B. 3963. A counter is travelling from the lower left corner to the upper right corner of the chessboard. It moves either one field to the right or one field up in each step. How many routes are there that pass through at least one of the four fields at the centre?
(4 pont)
solution (in Hungarian), statistics
B. 3964. The lengths of the legs in a right-angled triangle ABC are AC=3 and BC=4. The point A is shifted in a direction parallel to BC to the point A1, then the point B is shifted in a direction parallel to the line A1C to the point B1, and finally C is shifted in a direction parallel to A1B1 to the point C1. The resulting triangle A1B1C1 is right-angled at B1 and its leg A1B1 is 1 unit long. How long is the leg B1C1?
(3 pont)
solution (in Hungarian), statistics
B. 3965. On the sides AB and AC of an acute-angled triangle ABC as diameters, draw semicircles outside the triangle. The lines of the altitudes drawn from the opposite sides intersect the semicircles at M and N. Prove that AM=AN.
(3 pont)
solution (in Hungarian), statistics
B. 3966. In the chess tournament of a school, everyone played everyone else exactly once. Every player gained the same number of points playing against girls as playing against boys. Prove that the number of the participants is a perfect square. (1 point is due for winning, 0,5 for a draw, and 0 for losing.)
(5 pont)
solution (in Hungarian), statistics
B. 3967. Construct with ruler and compass, a triangle given is an angle and the lengths of the altitude and the median drawn from the vertex of that angle.
(4 pont)
solution (in Hungarian), statistics
B. 3968. Solve the following inequality:
(4 pont)
solution (in Hungarian), statistics
B. 3969. Determine the locus of the centres of all regular triangles circumscribed about a given acute triangle. (The triangle G is said to be circumscribed about the triangle H if the vertices of H lie on the sides of G.)
(5 pont)
solution (in Hungarian), statistics
B. 3970. Prove that the harmonic mean of the lengths of the diagonals of a regular heptagon of unit sides is 2.
(4 pont)
solution (in Hungarian), statistics
B. 3971. The sum of the non-negative numbers x, y, z is 1. Let
What are the maximum possible values of S and C?
(5 pont)
 |
Problems with sign 'A'Deadline expired on February 15, 2007. |
A. 416. In a right triangle ABC, point F is the perpendicular foot of C on hypotenuse AB. Let point Q on AB be the perpendicular foot of a certain point P on leg AC. The line through B which is perpendicular to BP intersects line CF at point R. Show that the intersection of circles with diameters AC and FQ, different from F, lies in the interior of segment PR.
(5 pont)
A. 417. n 3 people runs several rounds of race without any tie. Denote by f(n) the smallest possible number of rounds such that for any three people, all their six possible orders occur. Prove that ln n<f(n)<20ln n.
3 people runs several rounds of race without any tie. Denote by f(n) the smallest possible number of rounds such that for any three people, all their six possible orders occur. Prove that ln n<f(n)<20ln n.
(By Péter Pál Pach and Anna Puskás)
(5 pont)
A. 418. Show that for all pair of reals 0<a<b there exists a positive integer n such that
(Italian problem)
(5 pont)
Upload your solutions above.
