A KöMaL 2007. februári matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2007. március 16-án LEJÁRT. |
K. 115. Ha a számítógépen egyszerre több adatállományt (fájlt) jelölünk ki másolásra, majd elindítjuk a másolási folyamatot, ekkor két sávban láthatjuk a haladás mértékét. A felső sávban azt láthatjuk, hogy az éppen másolás alatt álló fájl méretének hány százalékánál tartunk, az alsó sávban pedig azt, hogy az összes másolandó fájl együttes méretéhez képest hány százaléknál tart a folyamat (az eddig átmásolt fájlokat is beleértve). Három fájl ilyen módon történő másolásakor a következőt látjuk: amikor az első fájlt másolja a gép, és a felső sávban 35% látható, akkor az alsó sávban 14% van; ha a második fájl másolásakor a felső sávban 24% van, akkor az alsó sávban 46%. Mit látunk a felső sávban, ha az alsó sávban 72% látható? (A megadott %-os értékek nem kerekítettek, hanem pontosak.)
(6 pont)
K. 116. Készítsünk egy pakli francia kártya lapjaiból 3×3-as bűvös négyzeteket (a bűvös négyzet mezőiben egy-egy kártyalap áll). A számozott lapok annyit érnek, amennyi rájuk van írva; a bubi értéke 11, a dámáé 12, a királyé 13, az ászé 1. A bűvös négyzetben egy-egy oszlopban, sorban, valamint átlóban álló három szám összege mindig ugyanannyi - ezt az összeget nevezzük ,,bűvös szám''-nak.
a) Mi a lehető legnagyobb bűvös szám, amit el lehet érni, ha csak 9 darab treffet használhatunk fel?
b) Lehet-e 37 a bűvös szám, ha bármelyik 9 lapot felhasználhatjuk?
(6 pont)
K. 117. Egy lapot az ábrának megfelelően a szaggatott vonalak mentén harmadára hajtjuk (mindkét hajtás tetszőleges ,,irányú'' lehet). A hajtásvonalak a lap két oldalát összesen hat részre osztják. Széthajtogatás után a hat rész mindegyikét különböző színűre színezzük, majd az eredeti hajtás mentén ismét összehajtjuk a lapot. Így csak két szín fog látszani, a két fedőlapon. Hány különböző színpárosítás valósítható meg különböző hajtogatásokkal?
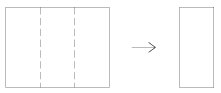
(6 pont)
K. 118. Adjuk meg az összes olyan ötjegyű számot, melynek számjegyei között pontosan a db 0, b db 1, c db 2, d db 3 és e db 4 szerepel. (A különböző betűk nem feltétlenül jelentenek különböző számjegyeket.)
(6 pont)
K. 119. Binumeriában két törzs él. A két törzs abban különbözik egymástól, hogy más számrendszert használnak. Megkérdeztünk mindkét törzsből egy-egy embert, hogy hányan élnek a törzsükben. Mindketten azt felelték, hogy 10011-en. Hányan élnek Binumeriában, ha mindkét törzsben 100-nál többen, de 1000-nél kevesebben élnek?
(6 pont)
K. 120. a) Adjunk meg egy olyan sokszöglapokkal határolt testet, melynek 12 csúcsa és 18 éle van.
b) Létezik-e a sokszöglapokkal határolt testek között olyan, melynek 12 csúcsa és 16 éle van?
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2007. március 19-én LEJÁRT. |
C. 885. Bankautomatából való pénzfelvétel költsége két részből tevődik össze. Van egy alapdíj, amely független a felvett összegtől. Ehhez járul a felvett összeggel egyenesen arányos rész. Mennyi a költség Ft felvétele esetén, ha
Ft esetén 221 Ft,
Ft esetén pedig 485 Ft?
(5 pont)
C. 886. Egy épület külsejének díszítése céljából egy nagyméretű négyzetet festettek a falra. Megrajzolták a négyzet körülírt körét és a négyzet oldalaira kifelé állított félköröket is. A körívek négy Hold alakú mezőt határolnak. Mekkora a négyzet oldala, ha egy-egy ilyen mező területe 1 m2?
(5 pont)
C. 887. Hány olyan nyolcjegyű szám van, amelyben minden előforduló számjegy pontosan annyiszor szerepel, amennyi a számjegy értéke? (Példa: .)
(5 pont)
C. 888. A 6 egység élű kocka felszínének és térfogatának a mérőszáma is 216. Adjuk meg az összes ilyen tulajdonságú négyzetes oszlopot, vagyis azokat, amelyeknek az élei egész hosszúságúak, továbbá a felszín és térfogat mérőszáma egyenlő.
(5 pont)
C. 889. Az ábrán felülnézetben látható csonkagúla alaplapjai téglalapok, magassága m. Valaki a csonkagúla térfogatára a következő képletet találta:
Igaz-e, hogy a képlet megadja a test térfogatát?
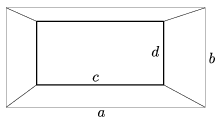
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2007. március 19-én LEJÁRT. |
B. 3972. Bizonyítsuk be, hogy egy n pozitív egészhez pontosan akkor adható meg n darab egész szám úgy, hogy összegük 0, szorzatuk pedig n legyen, ha n osztható 4-gyel.
(3 pont)
B. 3973. Hányféleképpen lehet a sakktáblán elhelyezni 14 futót úgy, hogy semelyik kettő ne üsse egymást?
(3 pont)
B. 3974. Adott egy ABC háromszög. Mi azon P pontok mértani helye a síkban, amelyekre AP2+BP2=CP2?
(4 pont)
B. 3975. Adott N és k pozitív egészekre megszámoltuk, hogy az N számot hányféleképpen lehet felírni a+b+c alakban, ahol 1 a,b,c
a,b,c k, és az összeadandók sorrendje is számít. Kaphattunk-e eredményül 2007-et?
k, és az összeadandók sorrendje is számít. Kaphattunk-e eredményül 2007-et?
(5 pont)
B. 3976. Az a, b, c oldalú háromszög egy belső pontján át húzzunk az oldalakkal párhuzamos egyeneseket. Ha ezek háromszögön belüli szakaszai egyenlő hosszúak, mekkora ez a hosszúság?
(4 pont)
B. 3977. Legyenek x, y, z pozitív valós számok, melyekre:
x2+xy+y2=2,
y2+yz+z2=5,
z2+xz+x2=3.
Határozzuk meg xy+yz+xz értékét.
(4 pont)
B. 3978. Bizonyítsuk be, hogy tetszőleges háromszögben érvényes az alábbi összefüggés:
2R(sa+sb+sc) a2+b2+c2.
a2+b2+c2.
(Itt a, b, c az oldalak, sa, sb, sc a súlyvonalak hossza, R pedig a háromszög köré írt kör sugara.)
(5 pont)
B. 3979. Az ABC háromszöget betűzzük pozitív körüljárás szerint. A háromszög szögei az A, B, illetve C csúcsnál rendre  ,
,  és
és  . A B csúcsot az A pont körül negatív irányban elforgatjuk
. A B csúcsot az A pont körül negatív irányban elforgatjuk  szöggel, majd az így kapott B1 pontot a B pont körül negatív irányban elforgatjuk
szöggel, majd az így kapott B1 pontot a B pont körül negatív irányban elforgatjuk  szöggel, és végül az így nyert B2 pontot a C pont körül negatív irányban
szöggel, és végül az így nyert B2 pontot a C pont körül negatív irányban  szöggel elforgatva a B3 pontba jutunk.
szöggel elforgatva a B3 pontba jutunk.
Szerkesszük meg a háromszöget, ha adottak a B, B3 pontok és az ABC háromszög beírt körének O középpontja. Vizsgáljuk meg azt is, hogyan alakul a megoldás a három adott pont elhelyezkedésétől függően.
(OKTV feladat nyomán)
(4 pont)
B. 3980. Az ábrán felülnézetben látható poliéder ,,alaplapjai'' párhuzamos téglalapok, oldalélei egyenlő hosszúak, magassága m. Valaki a poliéder térfogatára a következő képletet találta:
Igaz-e, hogy a képlet megadja a test térfogatát?
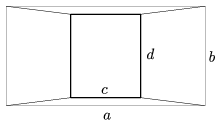
(3 pont)
B. 3981. Tegyük fel, hogy az ai, bi () valós számokra teljesülnek a következő egyenlőtlenségek:
továbbá , ha 1
 k
k n. Bizonyítsuk be, hogy
n. Bizonyítsuk be, hogy
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2007. március 19-én LEJÁRT. |
A. 419. Az ABCD húrnégyszög átlóinak metszéspontja X. Az ABX és CDX körök második metszéspontja Y. Vegyük fel a Z pontot úgy, hogy a BZC és AYD háromszögek hasonlóak legyenek. Mutassuk meg, hogy ha a BZCY négyszög konvex, akkor érintőnégyszög.
Orosz versenyfeladat
(5 pont)
A. 420. Határozzuk meg mindazokat az függvényeket, amelyekre tetszőleges x,y>0 esetén |f(x)-f(y)|
 |x-y|, és léteznek olyan a, b és c pozitív számok, amelyekre
|x-y|, és léteznek olyan a, b és c pozitív számok, amelyekre teljesül bármely x>0 esetén.
Javasolta: Dobribán Edgár, Kolozsvár
(5 pont)
A. 421. Mutassunk példát olyan  és c pozitív számokra, amelyekre
és c pozitív számokra, amelyekre
teljesül tetszőleges N pozitív egész esetén.
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

