A KöMaL 2007. áprilisi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2007. május 15-én LEJÁRT. |
I. 157. Rendszeres olvasóink bizonyára emlékeznek híres nyomozónkra, Fül Elek-re. Legutóbb (I. 134.) egy nyomozásához kérte segítségünket. Sajnos a ,,rosszfiúk'' megneszelték, hogy szorul a hurok, és adataikat most már titkosítva küldik egymásnak. Elek mindenképpen szeretné lefülelni őket, ehhez azonban meg kell fejtenie a titkos üzeneteket, és neki is képesnek kell lennie ilyen üzenetek írására. A kódolt üzenetek mindig csak pontosvesszővel elválasztott számokat tartalmaznak. A nyomozó megtudta, hogy a küldött üzeneteket mindig aláírják a gengszterek, ez alapján a
119; 25; 125; 69; 80; 118; 67; 147; 43; 21; 109; 29; 88; 128; 130; 72; 58; 156;
számsor Hack Elek aláírása. Fül Elek azonban észrevette azt is, hogy a számsor nem állandó, pl. a
112; 32; 36; 158; 63; 135; 97; 117; 44; 20; 51; 87; 58; 158; 49; 153; 83; 131;
számsor is Hack Elek nevének titkosítása. Feladatunk a következő: fejtsük meg, milyen módon titkosítják a bűnözők üzeneteiket, majd készítsünk programot, amely segít a detektívnek a rejtjeles üzenetek olvasásában, illetve új üzenet írásában. A program neve után három paraméter legyen: az első paraméter kötelezően a ,,be'' vagy ,,ki'' kifejezés, a be a titkosítást, a ki a megfejtést jelenti. Ezután a fájl neve, amiből az adatokat bekérjük, az utolsó paraméter pedig az elkészült üzenetfájl neve. Például: i157 ki titok.txt megfejt.txt a titok fájlt megfejti, és az eredményt a megfejt fájlban tárolja.
Beküldendő a program forráskódja (i157.pas, i157.cpp, ).
(10 pont)
I. 158. A galaktikus köztársaság központi csillagrendszeréről követek indulnak el, hogy a galaxis összes csillagrendszerébe személyesen elvigyék a köztársaság új lobogóját. A köztársaság vezetői úgy gondolják, hogy a lehető leggyorsabban úgy juttathatják el a lobogókat, ha minden egyes csillagrendszerbe követet küldenek egy hajón. Ekkor a központi csillagrendszertől legtávolabb lévő csillagrendszerbe érkezik meg utoljára a zászló.
Rájöttek azonban, hogy a csillagrendszerekbe megérkező követek tovább is indulhatnának. Sőt, arra is van lehetőség, hogy egy csillagrendszer felé több követ utazzon egy hajón, majd a zászló átadása után mindegyik követ más-más csillagrendszerek felé folytassa útját. Ehhez minden csillagrendszerben elegendő hajó áll rendelkezésre, melyek azonos sebességűek, és tetszőleges számú követet tudnak szállítani.
A köztársaság vezetése úgy döntött, hogy az utóbb leírt módon fogják indítani a követeket. Azt akarják elérni ugyanakkor, hogy a legtávolabbi csillagrendszer felé indított közvetlen hajó megérkezése előtt, vagy azzal egy időben, már az összes további csillagrendszerbe is elérkezzenek a zászlók. Tehát az utolsó lobogó átadásának ideje most sem lehet több, mint a közvetlen hajójáratok indítása esetén.
Számítsuk ki, hogy a közvetlen hajójáratokhoz képest legföljebb mennyivel csökkenthető a hajók összes útja a második követindítási stratégia alapján.
A csillagrendszerek adatait térbeli derékszögű koordinátákkal adjuk meg egy szöveges állományban. Az állomány minden egyes sora egy-egy csillagrendszer X, Y, Z valós koordinátáját tartalmazza egymástól szóközzel elválasztva. Az állomány első sorában a központi csillagrendszer adatai találhatók. A program a parancssorból olvassa be a bemeneti állomány nevét, majd a standard kimenetre írja a közvetlen hajójáratok összes útját, a legrövidebb hajójáratok összes útját, valamint a kettő különbségét.
Beküldendő a program forráskódja (i158.pas, i158. cpp, ) valamint a megoldás rövid dokumentációja (i158.txt, i158.pdf,
).
(10 pont)
I. 159. Egy fatelepen egyéni igényeknek megfelelő méretű gerendákat gyártanak. A megrendelők fix hosszúságú, de tetszőleges keresztmetszetű anyagot rendelhetnek. Az üzembe különböző átmérőjű rönkök érkeznek, ebből vágják ki a megfelelő alakokat. A gyártástechnológia miatt egy rönkből csak azonos méretű, és egymással párhuzamosan elhelyezkedő gerendákat vágnak. Egy lehetséges darabolást mutat az ábra.
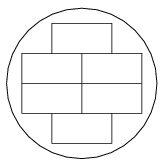
Készítsünk Excel táblázatot, amely segít kiválasztani három lehetséges vágásméret közül, hogy melyik méretből lehet a legkevesebb anyagveszteséggel a terméket legyártani. A munkafüzet két munkalapból álljon, az első oldalon a három lehetséges méret megadása szerepeljen: például 10 cm×20 cm; 15 cm×15 cm; 12 cm×17 cm, illetve a feldolgozásra váró nyersanyag átmérője (például 87 cm). Itt jelenjen meg a végeredmény is: melyik kivágás a legoptimálisabb az adott átmérőhöz. A másik munkalapon végezzük el a segédszámításokat.
A helyes megoldás mellett a felhasználóbarát megjelenést (pl. cellavédelem) is értékeljük.
(Cellavédelem esetén jelszó megadása nem szükséges.)
Beküldendő a megoldást tartalmazó munkafüzet. (i159.xls, ).
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2007. május 15-én LEJÁRT. |
S. 26. A Kincsfelderítő és -kiásó Intézet (KFKI) munkatársai régi kincsestérképeket és a modern technika legújabb vívmányait ötvözve végzik rég eltemetett értéktárgyak felszínre hozatalát.
Az intézet sokéves tapasztalata azt mutatja, hogy a kincsek java része karszthegységekben kerül elásásra, amelyek kemény kőzetében azonban barlangok találhatók. Ezek néhány kisebb-nagyobb, gömb alakúnak tekinthető - akár egymásba lógó - üregből állnak. A fúrás során e barlangokba lyukadva az a barlang tetszőleges másik pontjából folytatható, ily módon a ténylegesen fúrandó távolság lerövidíthető.
Írjunk programot, amely a terep szerkezetének ismeretében meghatározza, hogy a kincs kiásásához - az üregeket is kihasználva - optimális esetben mennyit kell fúrni és a fúrást a felszín mely pontjából kell indítani.
A program a kincs helyzetét és az üregek elhelyezkedését a standard bemenetről olvassa. A bemenet első sora az üregek N (0 N
N 1000) számát és a vízszintes síknak tekinthető felszín tengerszint feletti Yf magasságát tartalmazza. A második sor a kincs Xk, Yk, Zk koordinátáit, az ezt követő N sor pedig Xi, Yi, Zi, Ri alakban a földalatti üregeket írja le, ahol Xi, Yi, Zi az i-edik üreg középpontjának koordinátái, Ri pedig az üreg sugara. Feltehetjük, hogy minden üreg teljes egészében a föld alatt van.
1000) számát és a vízszintes síknak tekinthető felszín tengerszint feletti Yf magasságát tartalmazza. A második sor a kincs Xk, Yk, Zk koordinátáit, az ezt követő N sor pedig Xi, Yi, Zi, Ri alakban a földalatti üregeket írja le, ahol Xi, Yi, Zi az i-edik üreg középpontjának koordinátái, Ri pedig az üreg sugara. Feltehetjük, hogy minden üreg teljes egészében a föld alatt van.
A program az eredményt a standard kimenetre írja. Ennek egyetlen sora négy, tizedes tört alakban, legalább két tizedes pontossággal megadott számot tartalmazzon: a furat kezdőpozíciójának X, Y, Z koordinátáit és a minimálisan fúrandó L távolságot.

Beküldendő a program forráskódja (S26.pas, S26.cpp, ).
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

