A KöMaL 2007. májusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2007. június 11-én LEJÁRT. |
M. 279. Szeles időben könnyen lengésbe jönnek a villamos légvezetékek. A lengésidő függ a vezeték belógásától. Modellezzük a jelenséget egyetlen, adott hosszúságú hajlékony lánc belengetésével! Mérjük meg, hogy kis amplitúdójú lengések esetén hogyan függ a lengésidő a lánc belógásától!
Közli: Radnai Gyula, Budapest
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2007. június 11-én LEJÁRT. |
P. 3983. Egy gyalogló az edzésen az A és B pont között mozgott. Először A-ból B-be ment percenként 120 lépést téve meg, majd B-nél megfordult, s percenként 90 lépéssel jutott A-ba. Itt ismét megfordult, s percenként 60 lépést megtéve gyalogolt B-be, ahol visszafordult, s végül percenként 45-öt lépve gyalogolt el A-ig. A gyalogló edzése 1 óra 3 percet vett igénybe. Hány lépésre van A-tól B? Átlagosan hány lépést tett meg a gyalogló mozgása során percenként?
Közli: Zsigri Ferenc, Budapest
(3 pont)
P. 3984. Becsüljük meg, hogy mennyit változik a higanyoszlop magassága a Torricelli-kísérletben, ha
a) az eszközt a -os szobából kivisszük a teraszra, ahol
a hőmérséklet;
b) az eszközt bent hagyjuk a -os szobában, de néhány csepp vizet juttatunk a csőbe!
Közli: Zagyva Tiborné, Baja
(4 pont)
P. 3985. Két, egyenként m tömegű testet az ábrán látható elrendezésben  hosszú kötél köt össze, amely az asztal széléhez rögzített, negyedkör alakú csőben csúszik. Kezdetben a kötél
hosszú kötél köt össze, amely az asztal széléhez rögzített, negyedkör alakú csőben csúszik. Kezdetben a kötél része lóg függőlegesen. A súrlódástól mindenütt eltekinthetünk.
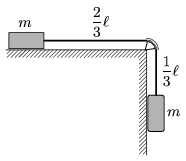
a) A rendszert magára hagyva mennyi idő alatt süllyed a jobb oldali test -et, és mekkora lesz ekkor a testek sebessége, ha a kötél tömege elhanyagolható?
b) Mekkora lenne a testek sebessége ugyanekkora út megtétele után, ha a kötél tömege is m volna?
Közli: Simon Péter, Pécs
(4 pont)
P. 3986. Az ábrán 0,3 mólnyi ideális gáz körfolyamata látható. A gáz hőmérséklete a 3. állapotban 900 K, a 4. állapotban 600 K.
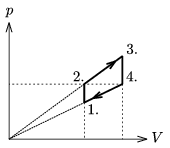
a) Mekkora a gáz hőmérséklete az 1. és a 2. állapotban?
b) Mennyi hasznos munkát végez a gáz a körfolyamat egyetlen ciklusa során?
Közli: Kotek László, Pécs
(4 pont)
P. 3987. Adott f fókusztávolságú gyüjtőlencsével egy tárgyról a tőle d távolságra lévő ernyőn valódi képet szeretnénk előállítani. Ábrázoljuk a lehetséges képek számát a d távolság függvényében!
Közli: Vágó Pál, Jászberény, Lehel Vezér Gimn.
(4 pont)
P. 3988. Vízszintes, feszes szigetelő pálcán súrlódásmentesen mozoghat egy m tömegű, q töltésű kicsiny gyöngy. A pálcától d távolságra helyezkedik el egy rögzített, Q nagyságú, q-val ellentétes előjelű pontszerű töltés. A gyöngyöt kissé kimozdítjuk egyensúlyi helyzetéből, majd magára hagyjuk. Mennyi lesz a kialakuló rezgőmozgás periódusideje?
Adatok: Q=10-8 C, q=-10-8 C, m=1 g, d=10 cm.
Közli: Cserti József, Budapest
(5 pont)
P. 3989. Egy, a fénysebesség 60%-ával mozgó proton rugalmasan szóródik egy másik, kezdetben nyugalomban lévő protonon. A szóródás után mindkét proton sebességvektora ugyanakkora szöget zár be a kezdetben mozgó proton mozgásirányával. Mekkora ez a szög, és mekkora sebességre tettek szert a protonok?
Közli: Varga István, Békéscsaba
(5 pont)
P. 3990. Két homogén testet a tömegközéppontjaikat összekötő egyenes mentén közelítve egymáshoz általában nő a két test közötti gravitációs vonzóerő. Mindig így van ez? Keressünk ellenpéldákat!
Orosz feladat
(4 pont)
P. 3991. Elég hosszú,  hajlásszögű lejtő aljától s távolságra egy R sugarú, m tömegű tömör hengert az ábrán látható irányban
hajlásszögű lejtő aljától s távolságra egy R sugarú, m tömegű tömör hengert az ábrán látható irányban  0 szögsebességgel megforgatva óvatosan a lejtőre helyezünk és kezdősebesség nélkül elengedünk. Milyen távolra jut el a henger a lejtő aljától, és mekkora sebességgel érkezik a lejtő aljára, ha
0 szögsebességgel megforgatva óvatosan a lejtőre helyezünk és kezdősebesség nélkül elengedünk. Milyen távolra jut el a henger a lejtő aljától, és mekkora sebességgel érkezik a lejtő aljára, ha
a)  =30o és
=30o és 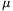 =0,2;
=0,2;
b)  =20o és
=20o és 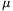 =0,4?
=0,4?
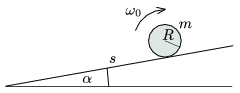
Adatok: s=2 m, R=0,2 m, 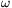 0=100 s-1.
0=100 s-1.
Közli: Holics László, Budapest
(5 pont)
P. 3992. R sugarú, M tömegű félgömb alakú homogén test súrlódás nélkül csúszhat a vízszintes asztalon. Tetejéről zérus kezdősebességgel indul egy m tömegű kis test, amely súrlódás nélkül lecsúszik róla.
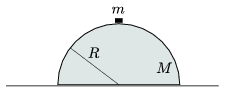
a) Mekkora sebességre gyorsul fel a félgömb?
b) Mekkora sebességgel és hol érkezik az asztalra a kis test?
Közli: Balogh Péter, Váchartyán
(5 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

