A KöMaL 2007. májusi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2007. június 15-én LEJÁRT. |
I. 160. Sokszor találkozunk az interneten hibás HTML oldalakkal, az egyik leggyakrabban előforduló probléma a parancsok hibás lezárása. Készítsünk programot, amelynek segítségével ellenőrizhetjük, hogy minden parancshoz elhelyeztünk-e záró tagot. A programunknak nem kell vizsgálnia, hogy létező parancsot adott-e ki a felhasználó, minden HTML szintaktika szerinti <parancs> </parancs> párt ellenőrizzen. Nem kell vizsgálnunk azt sem, hogy mely parancsoknak nincs záró eleme (pl.: <img src...>), azonban a hibás lezárási sorrend esetén jelezzen (pl.: <b><i></b></i>). A program paraméterként kapja az ellenőrzendő HTML fájl nevét (160.exe AKARMI.HTML), majd soronként ellenőrizze azt. Ha olyan parancsot talál, ami nem volt megnyitva, vagy a fájl végéig nem lett lezárva, vagy hibás a lezárási sorrend, akkor adjon hibaüzenetet. Az üzeneteket a hiba.txt nevű fájlban tároljuk, amit szintén a program hoz létre. A hibaüzenet a hibás sor sorszámát és a lezáratlan vagy meg nem nyitott parancsot tartalmazza.
Beküldendő a program forráskódja. (i160.pas, i160.cpp, ...)
(10 pont)
I. 161. Készítsünk ,,villám szimulátort'' az alábbi leírás alapján. A program paraméterként kapja a felhasználható képernyőterület nagyságát (pl.: I161.exe 30 20 esetén 30 karakter széles, 20 karakter magas területet használjunk). Töltsük fel a rendelkezésünkre álló képernyőt véletlenszerűen közötti számjegyekkel. Ezután a képernyő felső három sorában keressük ki, melyik oszlopban vagy oszlopokban maximális a számjegyek összege; ezekből a pontokból indul ki a villám. A villám mindig a legmagasabb szám irányában terjed, de csak vízszintesen, vagy lefelé: vagy vízszintesen halad, vagy függőlegesen lefelé, vagy átlósan lefelé. Ha azonos számot talál, mindkét irányban tovább terjed. Ha eléri a képernyő szélét (oldalt vagy alul), akkor kisül. A villám útját az általa érintett számok sárga színűre cserélésével jelezzük.
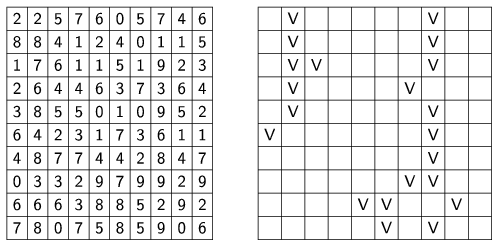
Az ábrán egy 10×10-es képernyőn a villám lefutása látható (a sárga számok helyét ,,V'' betűvel jeleztük).
Beküldendő a program forráskódja (i161.pas, i161.cpp, ...).
(10 pont)
I. 162. Készítsünk táblázatot egy rugóra erősített test egydimenziós csillapított rezgőmozgásának szimulációjához és a rezgés frekvenciájának megállapításához.
A táblázat első négy sora a rugóra erősített test tömegét (m), a rugó rugóállandóját (D), a csillapítási tényezőt (k), illetve a szimuláció két lépése közt eltelt időt (dt) tartalmazza. Az ezt követő sorokban a táblázat első négy oszlopában a szimuláció egyes időpontjaiban az eltelt idő, a test kitérése, sebessége és gyorsulása legyen kiszámolva. A szimuláció időtartama minél hosszabb legyen!
A rugó rezgésének frekvenciája a negyedik oszlop első sorában legyen meghatározva, a szimuláció alapján. A táblázatban szerepeljen egy grafikon is, amelyen látható a kitérés, a sebesség és a gyorsulás időfüggvénye.
A szimulációt lépésenként hajtsuk végre, minden lépésben kiszámolva a pillanatnyi gyorsulást, ebből meghatározva a pillanatnyi sebességet, illetve a pillanatnyi kitérést. A testre ható pillanatnyi eredő erő a test kitérésétől (x) és a sebességétől (v) függ:
F=-D.x-k.v.
Beküldendő a táblázat (i162.xls, ...).
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2007. június 15-én LEJÁRT. |
S. 27. Írjunk programot, amely a páros aknakereső játékban egy tetszőleges állásban lépést javasol.
A játék egy N×M-es táblán folyik, amelynek mezőin K db akna van elrejtve (egy mezőn legfeljebb csak egy). Kezdetben az összes mező felderítetlen. A játék során a két játékos felváltva választ egy-egy, még felderítetlen mezőt. Ha a kiválasztott mező aknát rejt, a játékos 1 pontot szerez, és újból választhat. Ellenkező esetben megtudjuk, hogy a kiválasztottal szomszédos 8 mező közül összesen hány rejt aknát - ez egy 0 és 8 közötti egész szám -, és a másik játékos következik. Kivételt képez az az eset, amikor a játékos olyan (aknamentes) mezőt derít fel, amely körül egy akna sincs, ugyanis ekkor az összes szomszédos mező is felfedésre kerül, illetve ha így olyan mező kerül felfedésre, amely körül szintén nincs egy akna sem, az eljárás rekurzívan ismétlődik. Természetesen ezután ebben az esetben is a másik játékos következik.
A játék végeztével, azaz az összes akna megtalálása után, az nyer, akinek több pontja van.
A program az aktuális játékállást a standard bemenetről olvassa. A bemenet első sorában három egész szám szerepel: a tábla N szélessége és M magassága, továbbá az elrejtett aknák K száma, egy-egy szóközzel elválasztva. Az ezt követő M sor mindegyike N karaktert tartalmaz: a bemenet (i+1)-edik sorának j-edik karaktere a játéktábla i-edik sorának és j-edik oszlopának kereszteződésében lévő mezőt írja le. Ez
- pont (.), ha a mező még federítetlen
- csillag (*), ha a mezőt már felderítette valamelyik játékos, és aknát tartalmaz
- 0 és 8 közötti számjegy, ha a mező már felderített, de nem rejtett aknát (ekkor ez az érték a mező szomszédságában lévő aknák száma).
A program a javasolt lépést - 10 másodpercen belül - a standard kimenetre írja. Ennek egyetlen sorában két, szóközzel elválasztott egész szám szerepeljen: a felderítendő mező X oszlop- és Y sorindexe (1 X
X N, 1
N, 1 Y
Y M).
M).
A működőképes megoldások között körmérkőzést rendezünk. A programok 10-20 játékból álló csoportokban mérik össze tudásukat, a csoport győztese az a program, amely a játékok legalább 2/3 részét nyeri. Ha ezt az arányt egyik program sem éri el, a csoport eredménye döntetlen. Mérkőzésenként a győztes 3 pontot kap, döntetlen esetén pedig mindkét játékos 1-1-et. A megoldásokat az így kialakult pontszám alapján rangsoroljuk, az első helyezett (megfelelő dokumentáció esetén) 10 pontot, a második 8-at, a többi megoldás legfeljebb 7 pontot kaphat. Kis különbségek esetén az első, illetve második helyen több megoldás is végezhet.
Feltehetjük, hogy a program bemenetére kizárólag helyes játékállás érkezik, továbbá, hogy N,M 100.
100.

Beküldendő a program forráskódja (s27.pas, s27.cpp, ... és dokumentációja).
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

