KöMaL Problems in Physics, November 2007
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on December 11, 2007. |
M. 282. By means of a compass measure the magnetic induction of a bar magnet as a function of the distance r measured from the centre of the magnet. The measurements should be carried out along two lines:
a) the longitudinal axis of the bar magnet;
b) perpendicularly to the longitudinal axis.
You may use that the horizontal component of the magnetic induction of the Earth is 2.10-5 T.
(6 pont)
 |
Problems with sign 'P'Deadline expired on December 11, 2007. |
P. 4013. By what percentage the gravitational force of the Earth is smaller at the height where the International Space Station orbits than at the surface of the Earth?
(3 pont)
P. 4014. Heat is continuously added to a sample of air in a cylinder closed by a piston, and the air is expanding at constant pressure. What fraction of the added heat increases the internal energy of the air, and what fraction of the added heat is converted to work?
(3 pont)
P. 4015. A physicist hanged a cylinder-shaped container of base 100 cm2 to a spring. He slowly poured water into the container and found that the surface of water remained at the same level. Find the spring constant D of the spring.
(4 pont)
P. 4016. The axle of a pulley of mass m=1 kg is attached to the end of a spring of spring constant D=200 N/m whose other end is fixed to the ceiling. A rope of negligible mass is placed to the pulley such that its left end is fixed to the ground and its right end is hanging freely from the pulley. At one moment we begin to pull the endpoint A at the right end of the rope by a constant vertical force of F=15 N. Friction can be neglected between the rope and the pulley.
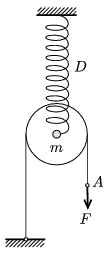
a) What is the initial elongation of the spring?
b) Find the greatest elongation of the spring.
c) Find the maximum displacement of point A.
(4 pont)
P. 4017. A tube of external diameter 2R and of unknown width is hanged by two threads of length  as shown in the figure. If the tube undergoes torsion oscillatory motion, the period T of the motion can be measured. Find the width of the wall of the tube.
as shown in the figure. If the tube undergoes torsion oscillatory motion, the period T of the motion can be measured. Find the width of the wall of the tube.
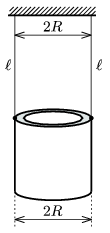
(5 pont)
P. 4018. Calculate the lattice constant of a body-centered cubic iron crystal using the molar mass of iron, the density of iron and the Avogadro number.
(4 pont)
P. 4019. A parallel plate condenser of charge Q consists of two vertical square-shaped plates of sides a, which are at a distance of d. Between the plates, parallel to them, there is another square-shaped metal plate which has the same size as the plates of the condenser and its width is d/3. Find the work done while this plate of density 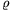 is pulled out of the plates.
is pulled out of the plates.
(5 pont)
P. 4020. A physicist works in a laboratory where the magnetic induction is 5 mT. She wears a golden necklace which encloses an area of 0.02 m2, and which has a resistance of 0.01 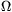 . What is the maximum of the current that flows in the necklace if the the magnetic induction decreases uniformly to 1 mT in 1 ms?
. What is the maximum of the current that flows in the necklace if the the magnetic induction decreases uniformly to 1 mT in 1 ms?
(4 pont)
P. 4021. The sharp image of the vertical filament of a bulb is projected to a white wall. How does the image change if a diffraction grating which consists of vertical slits is placed in the way of the light, right in front of the lens, or right behind the lens? Where can the wall be seen pure blue?
(5 pont)
P. 4022. Protons of kinetic energy 5.00 MeV are scattered totally elastically on the nuclei of an unknown element of negligible speed. The protons are deflected by 90o and their kinetic energy is 4.23 MeV.
a) What is the mass of the nuclei and what kind of chemical element's nuclei are they?
b) What is the direction of the motion of these nuclei with respect to the direction of the motion of the incident protons?
(5 pont)
Upload your solutions above.
