A KöMaL 2007. novemberi fizika feladatai

M-jelű feladatok A beküldési határidő 2007. december 11-én LEJÁRT.

---

M. 282. Mérjük meg egy iránytű segítségével a mágneses indukcióvektor nagyságát a rúdmágnes közepétől számított r távolság függvényében! Méréseinket két különböző egyenes mentén végezzük el:

a) a rúdmágnes hossztengelye mentén;

b) a rúdmágnes hossztengelyére merőlegesen!

Felhasználhatjuk, hogy a földi mágneses tér indukcióvektorának vízszintes összetevője 2^.10^-5 T nagyságú.

Varga István (1952-2007) feladata

(6 pont)

statisztika

P-jelű feladatok A beküldési határidő 2007. december 11-én LEJÁRT.

---

P. 4013. Hány százalékkal kisebb a Föld vonzóereje abban a magasságban, ahol a nemzetközi űrállomás kering, mint a Föld felszínén?

(Angol feladat)

(3 pont)

statisztika

---

P. 4014. Dugattyús hengerben lévő levegővel folyamatosan hőt közlünk, miközben a levegő állandó nyomáson tágul. A közölt hő hányad része növeli a levegő belső energiáját, és hányad része fordítódik munkavégzésre?

Közli: Légrádi Imre, Sopron

(3 pont)

statisztika

---

P. 4015. A kísérletező a 100 cm² alapterületű, hengeres edényt egy rugóra függesztette. Azt tapasztalta, hogy miközben az edénybe lassan vizet öntött, a víz szabad felszínének helyzete nem változott meg. Mekkora volt a D rugóállandó?

Közli: Bakonyi Gábor, Budapest

(4 pont)

statisztika

---

P. 4016. A mennyezethez rögzített, D=200 N/m direkciós erejű rugóra m=1 kg tömegű csiga tengelyét erősítjük. A csigán átvetett (elhanyagolható tömegű) fonál bal oldali, függőleges részének végét a talajhoz rögzítjük, jobb oldali része pedig szabadon lóg. Egy adott pillanatban a jobb oldali fonál végén levő A pontot állandó, F=15 N nagyságú, függőleges irányú erővel húzni kezdjük. A csiga és a fonál közötti súrlódás elhanyagolható.

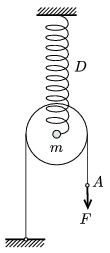
a) Mekkora a rugó kezdeti megnyúlása?

b) Határozzuk meg a rugó maximális megnyúlását!

c) Mekkora az A pont maximális elmozdulása?

Közli: Kotek László, Pécs

(4 pont)

statisztika

---

P. 4017. 2R külső átmérőjű, ismeretlen falvastagságú csövet függesztettünk fel két hosszúságú fonállal az ábra szerint. Ha a csövet kis kitérésű torziós lengésbe hozzuk, T lengésidőt mérhetünk. Mennyi a cső falának vastagsága?

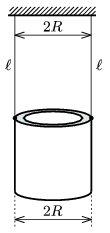
Közli: Gnädig Péter, Budapest

(5 pont)

statisztika

---

P. 4018. Számítsuk ki a térközepes kockarács elrendezésű vaskristály rácsállandóját a vas moláris tömegének, sűrűségének és az Avogadro-állandónak a felhasználásával!

Közli: Horváth István, Fonyód

(4 pont)

statisztika

---

P. 4019. Egy Q töltésű síkkondenzátor négyzet alakú, függőleges lemezeinek élhosszúsága a, a lemezek távolsága d. A lemezek között egy d/3 vastagságú, ugyanakkora négyzet alakú fémlemez helyezkedik el, a kondenzátor lemezeivel párhuzamosan. Mekkora munkával lehet ezt a sűrűségű fémlemezt függőlegesen kiemelni a kondenzátorból?

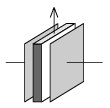
Nagy László fizikaverseny, Kazincbarcika

(5 pont)

statisztika

---

P. 4020. Egy fizikushallgató olyan laborban dolgozik, ahol 5 mT indukciójú mágneses tér van. Arany nyakláncot visel, amely 0,02 m² területet zár körbe, ellenállása 0,01 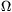. Legfeljebb mekkora áram folyik át a nyakláncon, ha a mágneses indukció 1 ms alatt egyenletesen 1 mT-ra csökken?

Tornyai Sándor fizikaverseny, Hódmezővásárhely

(4 pont)

statisztika

---

P. 4021. Függőleges izzószál éles képét vetítjük ki a fehér falra. Hogyan változik meg a vetítőlencse által előállított kép, ha egy függőleges résekből álló optikai rácsot helyezünk el a fény útjában, közvetlenül a lencse előtt, illetve a lencse mögött? Hol láthatjuk a falat tisztán kék színűnek?

Közli: Radnai Gyula, Budapest

(5 pont)

statisztika

---

P. 4022. 5,00 MeV mozgási energiájú protonok rugalmasan szóródnak elhanyagolható sebességű ismeretlen atommagokon. Az eredeti mozgásirányukhoz képest derékszögben eltérülő protonok mozgási energiája 4,23 MeV.

a) Mekkora az atommagok tömege, és melyik kémiai elem magjai lehetnek?

b) A beeső protonok irányához képest mekkora szögben szóródnak ezek a magok?

Wigner Jenő fizikaverseny, Békéscsaba

(5 pont)

statisztika