A KöMaL 2008. januári fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2008. február 11-én LEJÁRT. |
M. 284. Készítsünk hengerlencsét úgy, hogy különböző átmérőjű befőttesüvegeket vízzel töltünk tele! Hogyan függ a fókuszpont helye az átmérőtől?
Varga István (1952-2007) feladata
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2008. február 11-én LEJÁRT. |
P. 4033. Három telepet sorba kötünk. Elektromotoros erejük 2 V, 10 V, illetve 5 V; belső ellenállásuk 0,2 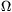 , 0,3
, 0,3 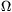 , illetve 0,5
, illetve 0,5 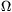 . Számítsuk ki és ábrázoljuk a harmadik telep kapocsfeszültségét a rendszerre kapcsolt külső terhelő ellenállás függvényében!
. Számítsuk ki és ábrázoljuk a harmadik telep kapocsfeszültségét a rendszerre kapcsolt külső terhelő ellenállás függvényében!
Közli: Veres Zoltán, Margitta (Románia)
(4 pont)
P. 4034. Egy  =30o hajlásszögű lejtőn lévő, m=1,8 kg tömegű testet a lejtővel párhuzamos fonállal a lejtő felső végéhez rögzítünk, majd a lejtőt vízszintes irányban a gyorsulással mozgatni kezdjük. A súrlódás elhanyagolható.
=30o hajlásszögű lejtőn lévő, m=1,8 kg tömegű testet a lejtővel párhuzamos fonállal a lejtő felső végéhez rögzítünk, majd a lejtőt vízszintes irányban a gyorsulással mozgatni kezdjük. A súrlódás elhanyagolható.
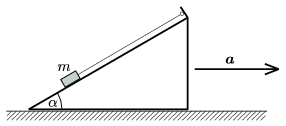
a) Mekkora a gyorsulás, ha a test erővel nyomja a lejtőt?
b) Mekkora a fonálerő?
Közli: Kotek László, Pécs
(4 pont)
P. 4035. Egy labda 1,5 m magasból leejtve 3 másodpercig pattog, majd megáll. Mekkora sebességgel kell a labdát folyamatosan pattogtatni, hogy az mindig visszaérkezzen 1,5 m magasra?
Közli: Simon Péter, Pécs
(4 pont)
P. 4036. Egy hosszú, könnyen gördülő kocsira v sebességgel rácsúszik egy ugyanakkora tömegű, elhanyagolható méretű test. A kocsi közepén egy R sugarú, nyolcadkörív keresztmetszetű lejtő csatlakozik érintőlegesen a platóhoz. A kis test felcsúszva a lejtőn éppen a kocsi végére esik. Milyen hosszú a kocsi? (A súrlódás mindenhol elhanyagolható.)
Adatok: v=5 m/s, R=0,4 m.
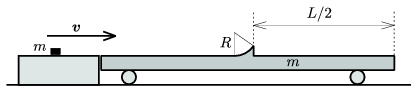
Közli: Holics László, Budapest
(5 pont)
P. 4037. Egy henger alakú lábosba lassan vizet töltünk. Az üres lábos tömegközéppontja 10 cm magasan van, a lábos tömege 1 kg, átmérője 20 cm. Milyen magasan áll benne a víz, amikor a rendszer tömegközéppontja a legmélyebben van? Ebben az esetben a víz felszínéhez képest hol helyezkedik el a közös tömegközéppont?
Közli: Légrádi Imre, Sopron
(5 pont)
P. 4038. A korszerű szennyvíztisztító telepeken ülepítéssel nyernek magas szervesanyag-tartalmú biomasszát. Ebből baktériumok anyagcseréjét felhasználva állítják elő az úgynevezett biogázt, és azt folyadékdugós gáztartályban tárolják. (A gáztartály egy lefordított, vízben álló pohárhoz hasonlítható.) Ha a gáz mennyiségét növelik, akkor a tartály megemelkedik; ha a gázból kiengednek, a tartály megsüllyed. A gáz távozását a tartályban levő folyadékoszlop, a folyadékdugó gátolja meg. Biztonsági okokból a folyadékdugó h magasságának legalább 1 méternek kell lennie, és a felső lap legfeljebb H=6,5 méternyire emelkedhet a külső vízszint fölé.
A keletkezett gáz térfogatának 60%-a metán, 40%-a szén-dioxid. Az üres, henger alakú tartály térfogata 2000 m3, a tárolt gáz túlnyomása 50 mbar, és a nyári kánikulában a napsugárzás következtében a gáz maximálisan 60 oC-os hőmérsékletet érhet el.
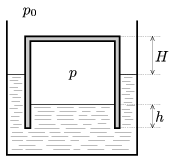
a) Hány tonna a mozgó rész tömege?
b) Hány köbméter p=1,013 bar nyomású, 20 oC hőmérsékletű gázt juttathatnak a tartályba?
c) Mennyi hő szabadul fel a teljes gázmennyiség elégetésekor?
Az átlagos külső nyomás p0=1,013.105 Pa.
Közli: Zagyva Tiborné, Baja
(5 pont)
P. 4039. Egy 80 l térfogatú edényben 402 oC hőmérsékletű, 4,2.105 Pa nyomású, 192 g tömegű gáz van, amelynek állandó térfogaton mért hőkapacitása 124,5 J/K.
a) Hány szabadsági fokúak a gázmolekulák?
b) Milyen gáz lehet az edényben?
Közli: Zsigri Ferenc, Budapest
(4 pont)
P. 4040. Tervezzünk 6 V-os telepről táplált világító diódás (LED-es) áramkört, amelynek különböző színű diódái 2 V, 3 V, illetve 4 V feszültségre nyitnak, és áramuk 10 mA. Bármely felhasznált ellenállás évente 1% és bármely színű LED évente 3% valószínűséggel hibásodik meg. Mennyi a valószínűsége annak, hogy az áramkör az első évben hibamentesen működik?
Közli: Bakonyi Gábor, Budapest
(4 pont)
P. 4041. Egy m tömegű, 2 hosszúságú, vékony, homogén rúd R sugarú, függőleges síkú körben mozoghat súrlódás nélkül. Határozzuk meg az egyensúlyi helyzet körüli kis rezgés frekvenciáját!
hosszúságú, vékony, homogén rúd R sugarú, függőleges síkú körben mozoghat súrlódás nélkül. Határozzuk meg az egyensúlyi helyzet körüli kis rezgés frekvenciáját!
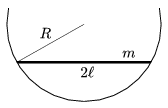
Közli: Gálfi László, Budapest
(5 pont)
P. 4042. Egy 40 W-os izzólámpa a felvett elektromos energia 2%-át alakítja át látható fénnyé. Tegyük fel, hogy egyetlen foton kibocsátásának átlagos ideje 10-14 másodperc. Átlagosan hány látható foton hagyja el az izzószálat egyszerre?
Közli: Radnai Gyula, Budapest
(4 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

