KöMaL Problems in Physics, April 2008
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on May 13, 2008. |
M. 287. Blow air through a straw steadily and measure the speed of the flowing air.
(6 pont)
 |
Problems with sign 'P'Deadline expired on May 13, 2008. |
P. 4064. Hansel and Gretel live in Gingerbread street 21. Once Gretel visited Little Red Riding Hood, she left home at 10 past 8. Gretel was walking at a constant speed of 3 km/h. Hansel noticed that Gretel left Little Red Riding Hood's present at home, so at 20 past 8 he also left home and ran after Gretel at a speed of 5 km/h to give her the present. He was lucky and reached Gretel before she got to Little Red Riding Hood's house. At least how far does Little Red Riding Hood live from Gingerbread street 21?
(3 pont)
P. 4065. By what percent does the resistance of a mercury column increase if it is placed into another tube in which its length increases by p percent?
(3 pont)
P. 4066. An object can be hanged to a 5-m long wire of diameter 2 mm, and the wire does not break. However, if the object is displaced a bit and begins to swing, the wire breaks. Why? If another piece of wire having the same length and material but wider diameter is used, the speed of the swinging object can even be 7 m/s. Calculate the least diameter of this wider wire.
(4 pont)
P. 4067. You may put your finger 1-2 mm close to the side of the flames of a burning candle. Why?
(4 pont)
P. 4068. In a circus performance one of the acrobats falls freely from a height of 10 m. When and with what speed should the other acrobat jump up from the springboard, such that they pass each other halfway, with having the same speed? Plot the position versus time and velocity versus time graphs of the motions of both acrobats.
(4 pont)
P. 4069. The figure shows a circular trough in a vertical plane. A small object is started at point A with a vertically downward initial velocity, such that it runs along the trough until it reaches point B, at which it takes off, and then it falls back exactly to point A. What is the maximum value of the angle  ? (Air resistance is negligible.)
? (Air resistance is negligible.)
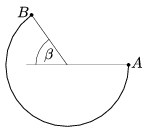
(5 pont)
P. 4070. A sample of ideal gas of 1 mole expands at constant pressure, during which it absorbs 100 J thermal energy, and its temperature increases by 4 oC. What kind of molecules may the gas contain?
(4 pont)
P. 4071. Newton recognized that if the object and image distances are not measured from the pole of the spherical mirror but from another point the curved mirror formula can be written in the following form: t*.k*=f2. (t* and k* are the new object and image distances, respectively.) From which point did Newton measured the image and the object distances?
(4 pont)
P. 4072. Two pointlike particles of charge Q are fixed at two of the vertices of an equilateral triangle of sides  . At the third vertex a third particle of mass m and of charge q is released.
. At the third vertex a third particle of mass m and of charge q is released.
What is the initial acceleration of this particle, and with what speed does it pass one of the the points which is at a distance of 2 from both the fixed charges? How does the result change if the effect of the gravitational force is considered as well while the particle moves along a vertical line?
from both the fixed charges? How does the result change if the effect of the gravitational force is considered as well while the particle moves along a vertical line?
Data:  =10 cm, m=10-3 g, Q=10-8 C, q=10-9 C.
=10 cm, m=10-3 g, Q=10-8 C, q=10-9 C.
(5 pont)
P. 4073. An electrometer is charged to 3 kV. Then the electrometer is touched with an - initially neutral - metal ball, mounted on an insulating rod, and then the metal ball is taken away and earthed. The process is repeated 10 times, and finally the electrometer reads 1.5 kV. After this, at least how many times must the above process be repeated in order that the electrometer reads less than 1 kV?
(5 pont)
Upload your solutions above.
