A KöMaL 2008. novemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2008. december 15-én LEJÁRT. |
I. 196. Keressük meg a egyenlet legkisebb abszolút értékű gyökét legalább 12 tizedes jegy pontossággal.
Beküldendő az egyenlet legkisebb abszolút értékű gyöke és a feladat megoldási menetének leírása (i196.txt, i196.pdf, ...), valamint minden egyéb, a megoldás során fölhasznált saját készítésű számítógépes termék (ábra, forráskód, táblázat, ...).
(10 pont)
I. 197. Egy áruházban N különféle terméket szeretnénk megvenni, több részletben, minden alkalommal néhány terméket megvásárolva. Írjunk programot, mely a termékek árainak ismeretében meghatározza, hogy azokat milyen felosztásban vegyük meg ahhoz, hogy az egyes vásárlások során az 5-ösökre való kerekítésből adódó hibák összességében számunkra a lehető legnagyobb megtakarítást eredményezzék.
A program a termékek számát és árait a standard bemenetről olvassa. Minden sorban egy-egy bevásárlólista leírása szerepel: a megvásárolni kívánt termékek N száma, majd a1,...,aN, szóközzel elválasztott pozitív egész számok, a termékek árai. Egy listán a termékek árösszege legfeljebb
, a bemenet végét egy ,,0'' tartalmú sor jelzi.
A program bevásárlólistánként egy sort, ebben pedig egyetlen számot írjon a standard kimenetre: az adott listán szereplő összes termék optimális felosztásban történő megvásárlása esetén a kerekítési hibákból adódó összes hasznunkat vagy veszteségünket.
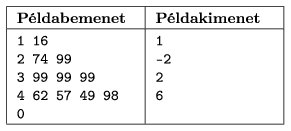
Beküldendő a program forráskódja (i197.pas, i197.cpp, ...), valamint a program rövid dokumentációja (i197.txt, i197.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztőkörnyezetben fordítható.
(10 pont)
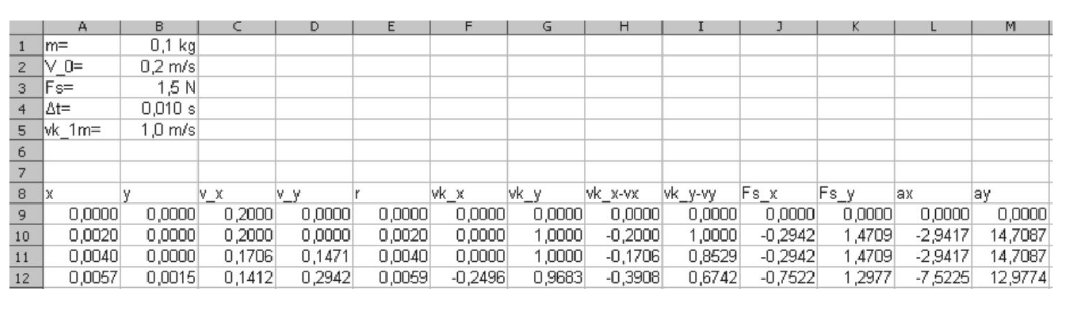
I. 198. Szimuláljuk táblázatkezelő segítségével egy vízszintes, egyenletesen forgó korong közepéről elindított m tömegű test mozgását. A korong az óramutató járásával ellentétes irányban forog függőleges szimmetriatengelye körül, bármely pontjának vk sebessége (ún. kerületi sebessége) a középpontból az adott pontba húzott egyenesre merőleges irányú, nagysága a középponttól mért távolsággal egyenesen arányos. A pontszerűnek tekinthető, m tömegű testet a korong középpontjából indítjuk V0 kezdősebességgel, majd magára hagyjuk. A testre ezután (vízszintesen) csak a korong által kifejtett állandó nagyságú Fs csúszási súrlódási erő hat, melynek iránya ellentétes a test koronghoz viszonyított sebességével.
Vizsgáljuk a folyamatot egy olyan derékszögű koordináta-rendszerben, melynek origója a korong középpontja, és az x tengely V0 irányába mutat. A szimulációt úgy végezzük, hogy a folyamatot 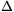 t nagyságú időközökre osztjuk, mely időközökön belül a vizsgált fizikai mennyiségeket állandónak tekintjük. A kiindulási állapot után bármely időpont aktuális értékeiből a
t nagyságú időközökre osztjuk, mely időközökön belül a vizsgált fizikai mennyiségeket állandónak tekintjük. A kiindulási állapot után bármely időpont aktuális értékeiből a 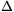 t-vel későbbi időpont értékeit a következő módon számítjuk ki:
t-vel későbbi időpont értékeit a következő módon számítjuk ki:
a test helyzetét leíró x és y koordinátákat minden esetben az előző időszak vx és vy sebességkoordinátáinak
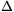 t-szeresével növeljük;
t-szeresével növeljük;
kiszámítjuk a test középponttól mért r távolságát, valamint a korong adott pontbeli sebességének vkx és vky összetevőit;
kiszámítjuk a korong testtel érintkező pontja és a test sebességvektorainak különbségét, mivel ezzel egyező irányú lesz a testre ható súrlódási erő;
kiszámítjuk a súrlódási erő komponenseit, majd a segítségükkel a gyorsulások koordinátáit;
a gyorsulások komponenseit
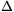 t-vel szorozva megkapjuk a sebességváltozásokat: ezekkel növeljük a következő szimulációs lépésben a sebességet.
t-vel szorozva megkapjuk a sebességváltozásokat: ezekkel növeljük a következő szimulációs lépésben a sebességet.
A test tömegét, a kezdeti sebességet, a súrlódási erő nagyságát, a szimulációs lépések között eltelt időt és a korong középponttól 1 méterre lévő pontjának kerületi sebességét a táblázat első öt sorában adjuk meg a mintának megfelelően. A táblázat további soraiban a test mozgását leíró mennyiségek legalább 300 értékét számítsuk ki, és a mozgás pályáját ábrázoljuk megfelelő diagramon.
Beküldendő a táblázatkezelő munkafüzet (i198.xls, i198.ods, ...), illetve egy rövid dokumentáció (i198.txt, i198.pdf, ...) amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziója, valamint a megoldás rövid leírása.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2008. december 15-én LEJÁRT. |
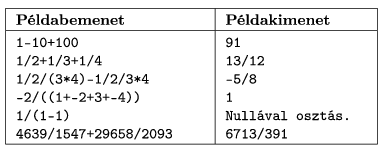
S. 39. Készítsünk számológépet, mely képes összetett számtani kifejezések kiértékelésére. A kifejezésekben egész számok, zárójelek és a négy alapművelet jele (+,-,*,/) szerepelhetnek. A műveleti sorrend a szokványos legyen: a szorzás és osztás egyenrangúak, és megelőzik az összeadást és a kivonást, melyek szintén egyenrangúak. Ezen kívül, ha zárójelek másként nem jelölik, a halmozott egyenrangú műveleteket mindig balról jobbra értékeljük ki. Tehát például: e-f-a/b/c*d=(e-f)-(((a/b)/c)*d).
A program a kiértékelendő kifejezéseket fájlból olvassa, és az eredményeket fájlba írja. A bemeneti, illetve a kimeneti fájlok nevei az első, illetve második parancssori argumentumok. A bemenet minden sorában egy-egy kifejezés szerepel. A kimenetben minden kifejezéshez egy-egy sor tartozzon, melyben egyetlen (tört)szám, a kifejezés pontos értéke szerepeljen, legegyszerűbb alakra hozva. Ha a kifejezés kiértékelése közben 0-val osztás történne, akkor a sorba a ,,Nullával osztás.'' szöveg kerüljön.
Feltehetjük, hogy egy sor legfeljebb 250 karakter hosszú, a kifejezések szintaktikailag helyesek, és hogy a számítás során (mindig a legegyszerűbb alakra hozva) minden részeredmény leírható két 16-bites egész szám hányadosaként. Figyeljünk azonban arra, hogy a műveletek elvégzése közben se fordulhasson elő túlcsordulás, szükség esetén használjunk 32 bites számokat!
Beküldendő a program forráskódja (s39.pas, s39.cpp, ...), valamint a program rövid dokumentációja (s39.txt, s39.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztőkörnyezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

