A KöMaL 2008. decemberi matematika feladatai

Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.

Feladat típusok elrejtése/megmutatása:

K-jelű feladatok

A beküldési határidő 2009. január 10-én LEJÁRT.

K. 187. Töltsük ki az ábra üres celláit úgy, hogy bármely három, egy csúcsban egymással érintkező kis hatszögben álló számok összege mindig ugyanannyi legyen.

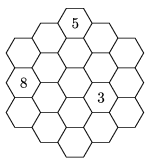
(6 pont)

megoldás, statisztika

K. 188. Az ABC egyenlő szárú háromszög AB alapját a B csúcson túl meghosszabbítottuk a szár hosszával. Az így kapott pont lett a C₁. Az AB alapra az A csúcsban merőlegest állítottunk, majd a C-t tartalmazó félsík irányába a merőleges egyenesre felmértük a szár hosszát. Az így kapott pont lett a C₂. Azt tapasztaltuk, hogy a C₁, C és C₂ pontok egy egyenesre illeszkednek. Határozzuk meg az ABC háromszög szögeit.

(6 pont)

megoldás, statisztika

K. 189. Egy gyakorló órán a matematikatanár ötféle feladatot tűzött ki, minden fajtából három darabot. Egy feladat jó megoldásáért 1 pontot kapnak a tanulók, ha nem oldottak meg ebből a fajtából többet. Ha két jó megoldásuk van egy fajtából, akkor ezekre feladatonként 4 pontot, ha mindhárom megvan egy fajtából, akkor ezekre feladatonként 9 pontot kapnak.

A feladatmegoldásban a tanulók csapatokban vettek részt. A végén minden csapatnak a többiekétől különböző pontszáma alakult ki, de minden csapat pontszáma 3-mal osztható lett. Legfeljebb hány csapat vehetett részt a feladatmegoldásban?

(6 pont)

megoldás, statisztika

K. 190. Egy szavazáson a fiúk 55%-a, a lányok 5%-a szavazott igennel, így a többség igennel szavazott. Legalább hány fiú szavazott nemmel?

(6 pont)

megoldás, statisztika

K. 191. Kétféle ablaktörlőt vizsgálunk, mindkettőnél a 31 cm-es törlőlapát a közepénél egy szintén 31 cm hosszú nyélre van rögzítve, amelyik egy tengely körül 90^o-ot fordul törlés közben. Az első típusnál a rögzítés fix, így a törlő kezdetben 45^o-ot zár be az ablak aljával, és törlés közben a lapát mindig a nyél irányába mutat. A másik típusnál a rögzítésnél csukló van, így a törlő végig merőleges az ablak aljára a törlés alatt. Melyik típusú ablaktörlő töröl le nagyobb területet?

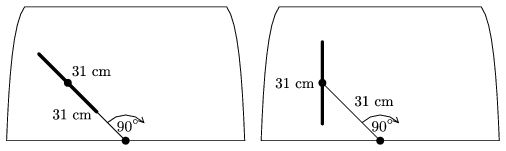
(6 pont)

megoldás, statisztika

K. 192. Anna, Bori és Cili egy hat darab igaz-hamis kérdésből álló tesztet töltött ki (mindannyian ugyanarra a hat kérdésre válaszoltak). Anna válaszai sorrendben: H, H, I, I, I, I; Bori válaszai sorrendben I, H, H, I, I, I, Cili válaszai sorrendben I, I, H, H, I, I. Annának csak két rossz, Borinak csak két jó válasza volt. Hány helyes válasza lehet Cilinek?

(6 pont)

megoldás, statisztika

C-jelű feladatok

A beküldési határidő 2009. január 15-én LEJÁRT.

C. 965. Az ábrasorozat mintája fekete, fehér és szürke négyzetekből áll.

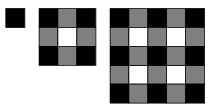
Hányadik ábrán lesz 2112 darab szürke négyzet?

(5 pont)

megoldás, statisztika

C. 966. A magyar rendszámokban a számjegyek között lehetnek azonosak is. Valaki a megfigyelései alapján azt a kijelentést tette, hogy szerinte átlagosan 10 gépjárműből közel 3-nak ilyen a rendszáma. Igaz-e ez az állítás?

(5 pont)

megoldás, statisztika

C. 967. Oldjuk meg az alábbi egyenletrendszert:

3x²-xy=1,

9xy+y²=22.

(5 pont)

megoldás, statisztika

C. 968. Az ABCD négyzetet az ábrán látható módon az oldalaival párhuzamos egyenesekkel az NPLD és KBMP négyzetekre és két egybevágó téglalapra osztottuk.

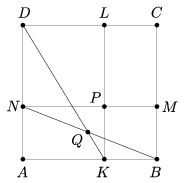
Legyen KL és MN metszéspontja P, BN és DK metszéspontja pedig Q. Mutassuk meg, hogy a C, P és Q pontok egy egyenesre illeszkednek.

(5 pont)

megoldás, statisztika

C. 969. Egy körző szárait kétszer akkora szöggel kell kinyitnunk, ha 6,5 cm sugarú kört akarunk rajzolni, mint ha 3,3 cm sugarú kört rajzolunk. Milyen hosszú a körző szára?

(5 pont)

megoldás, statisztika

B-jelű feladatok

A beküldési határidő 2009. január 15-én LEJÁRT.

B. 4132. Aranka és Bianka egy 2008×2008-as sakktáblán a következő játékot játsszák. Aranka gondolatban kiválasztja a tábla néhány mezőjét. Ezután minden mezőre ráírja, hogy az és a vele éllel vagy csúccsal érintkező mezők közül összesen hány szerepel a kiválasztottak között. Meg tudja-e határozni ennek alapján Bianka, hogy mely mezőket választotta ki Aranka? Mi a helyzet, ha 2009×2009-es táblán játszanak?

Javasolta: Nagy Dániel

(5 pont)

megoldás, statisztika

B. 4133. Az ABCD téglalap BC és CD oldalán a P és Q pont úgy helyezkedik el, hogy az APQ háromszög szabályos. Bizonyítsuk be, hogy t_AQD+t_ABP=t_PCQ.

(3 pont)

megoldás, statisztika

B. 4134. Egy $a_1<a_2<\ldots<a_k$ sorozatra jelölje $t_3(a_1,\ldots,a_k)$ a sorozat elemeiből kiválasztható háromtagú számtani sorozatok számát. Bizonyítandó, hogy $t_3(a_1,\ldots,a_k)\le t_3(1,2,\ldots,k)$ .

(4 pont)

megoldás, statisztika

B. 4135. Az ABCD négyzet belsejében úgy helyezkedik el az M pont, hogy $DCM\sphericalangle= MAC\sphericalangle=25^{\circ}$ . Mekkora az ABM szög?

(4 pont)

megoldás, statisztika

B. 4136. Adott egy konvex négyszög. Szerkesszünk rombuszt, amelynek csúcsai a négyszög oldalaira esnek, oldalai pedig párhuzamosak a négyszög átlóival.

(3 pont)

megoldás, statisztika

B. 4137. Legyen n pozitív egész szám. Igazoljuk, hogy

$\sum_{0\le k<n/2} \binom{n}{2k+1} 13^k$

osztható 2^n-1-nel.

(5 pont)

megoldás, statisztika

B. 4138. Oldjuk meg a következő egyenletet:

$\sqrt{2}\cdot (\sin x+\cos x)= \mathop{\rm tg} x+ \mathop{\rm ctg} x.$

(4 pont)

megoldás, statisztika

B. 4139. Az ABC hegyesszögű háromszög két magasságvonala BE és CF. Az EF egyenes a körülírt kört P-ben és Q-ban metszi. Bizonyítsuk be, hogy AP=AQ.

(4 pont)

megoldás, statisztika

B. 4140. Az ABCD húrnégyszög a körülírt körén a BC ív felezőpontja E, a DA ív felezőpontja F. Az ABC háromszög beírt körének középpontja legyen P, az ABD háromszögé Q. Mutassuk meg, hogy PQ párhuzamos EF-fel.

(4 pont)

megoldás, statisztika

B. 4141. Igazoljuk, hogy tetszőleges a, b, c valós számokra teljesül

(a²+2)(b²+2)(c²+2) $\ge$ 3(a+b+c)².

(5 pont)

megoldás, statisztika

A-jelű feladatok

A beküldési határidő 2009. február 16-án LEJÁRT.

A. 467. Az ABCD érintőtrapéz AD és BC oldalegyenesei az R pontban metszik egymást. A beírt kör középpontja I, a kör az AB oldalt a P, a CD oldalt a Q pontban érinti. A P-ben PR-re állított merőleges A₁-ben, illetve B₁-ben metszi az AI és BI szögfelező egyeneseket. Hasonlóképpen, a Q-ban QR-re állított merőleges C₁-ben, illetve D₁-ben metszi a CI és DI egyeneseket. Mutassuk meg, hogy A₁D₁=B₁C₁.

Javasolta: Bohner Géza, Budapest

(5 pont)

statisztika

A. 468. Adott két háromszög. Az oldalaik a, b, c, illetve A, B, C; területük t, illetve T. Igazoljuk, hogy

-a²A²+a²B²+a²C²+b²A²-b²B²+b²C²+c²A²+c²B²-c²C² $\ge$ 16tT.

(5 pont)

megoldás, statisztika

A. 469. Legyenek 0 $\le$ k $\le$ n és m $\ge$ 2 egészek. Tekintsük az $\{1,2,\ldots,n\}$ halmaz k-elemű részhalmazait, és minden egyes ilyen részhalmazban az elemek összegének osztási maradékát m-mel osztva. Bizonyítsuk be, hogy ha az m-féle maradék mindegyike ugyanannyiszor, azaz pontosan $\frac{\binom{n}{k}}{m}$ -szer fordul elő, akkor n $\ge$ m.

(5 pont)

megoldás, statisztika

A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:

megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.

(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

Már regisztráltál?
Új vendég vagy?