A KöMaL 2009. márciusi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2009. április 10-én LEJÁRT. |
K. 205. Jancsi és Juliska a tőlük 20 km-re levő mézeskalácsházhoz igyekszik. Kettejüknek van egy biciklijük, amin egyszerre csak egyikük tud ülni. Elhatározták, hogy először Jancsi fog gyalogolni, és Juliska biciklizik valameddig, ott leteszi a biciklit, majd gyalog megy tovább. Amikor Jancsi odaér, felszáll a biciklire, és elmegy vele a mézeskalácsházig. Jancsi 5 km/h sebességgel gyalogol és 12 km/h sebességgel biciklizik, Juliska 4 km/h sebességgel gyalogol, és 10 km/h sebességgel biciklizik. Hány km-t kell Juliskának bicikliznie, hogy egyszerre érjenek a mézeskalácsházhoz, ha egyszerre is indulnak el?
(6 pont)
K. 206. Pisti és Karcsi testvérek. Egy nap édesanyjuk a cukrászdából 8 db nagyobb, és 27 db kisebb mignont vitt haza. A nagyobb mignon alakja 3 cm oldalhosszúságú kocka, a kisebbé pedig 2 cm oldalhosszúságú kocka. Minden mignon 5-5 oldallapja cukormázzal van borítva azonos vastagságban, az aljukra nem tettek mázat. Karcsi és Pisti úgy szeretné elosztani a mignonokat, hogy mindkettőjüknek azonos össztérfogatú mignon jusson, mindketten kapjanak mindkét féléből, és abban is megegyeznek, hogy egyik mignont sem darabolják fel.
a) Mutassuk meg, hogy ilyen feltételekkel történő elosztás nem lehetséges.
b) Mivel látták, hogy tészta szerint nem tudják igazságosan elosztani a mignonokat, megállapodnak, hogy úgy osztják el a mignonokat, hogy mindkettőjüknek azonos mennyiségű cukormáz jusson. (Továbbra sem lehet feldarabolni egyik mignont sem, és mindkettőjüknek kell kapnia mindkét féléből.) Adjuk meg az összes megfelelő elosztási lehetőséget.
(6 pont)
K. 207. Egy 14,4 m2 alapterületű téglalap alakú folyosót egyforma téglalap alakú csempékkel raktak ki úgy, hogy hosszában haladva minden ötödik sorban derékszögben elfordítva tették le a csempéket. Így 15 sor csempét kellett lerakni, vágás nélkül. Később észrevették, hogy ha végig úgy teszik a csempéket, mint az ötödik sorokban van, akkor sem kell vágni, csak ekkor 18 sor kell. Milyen méretű csempékkel dolgozhattak, ha a csempék oldalai cm-ben egész számok?
(6 pont)
K. 208. a) Egy koordinátarendszerben megrajzoltuk az origó középpontú, 5 egység sugarú kört. Hány rácspont esik erre a körvonalra? (Rácspontnak nevezzük azokat a pontokat, melyeknek mindkét koordinátája egész szám.)
b) Adjunk meg olyan r egész értéket, melyre az origó középpontú, r sugarú körvonalon több, mint 14 rácspont található. Mutassuk is meg, hogy a megadott r érték eleget tesz a feltételnek.
(6 pont)
K. 209. Egy kereskedő a fagylaltárusító pavilonjára körbe falemezből készült árnyékoló előtetőt szeretne szereltetni. Az előtetővel ellátott pavilon látszati és felülnézeti képét az ábrán láthatjuk. Az előtető egy-egy darabjának síkja a pavilon megfelelő függőleges oldalfalával 45o-os szöget zár be. A pavilon alapja 3 m oldalhosszúságú négyzet. Az előtető a fal síkjától merőlegesen számított 1 m távolságig nyúlik ki. Hány m2 falemez kell az előtető elkészítéséhez?
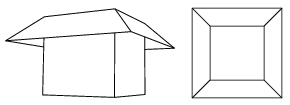
(6 pont)
K. 210. Az ábrán Dóri kisbiciklijének részlete látható. A hátsó kerék középpontja A, a TK hajtókar (melynek végén található az egyik pedál) pedig a T pont körül forog. Tekintsük az A, K, T pontokat egysíkúnak. A TK hossza 20 cm, AT hossza 48 cm. Hány olyan helyzete van a K pontnak, miközben a hajtókar T körül körbefordul, amikor az AK távolság cm-ben mérve egész szám, és az AKT háromszög hegyesszögű?
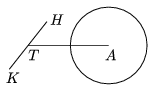
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2009. április 15-én LEJÁRT. |
C. 980. Tételezzük fel, hogy az allergiások között viszonylag több a tizenéves, és a tizenéveseknek az átlagosnál nagyobb hányada sportol. Következik-e ebből, hogy a sportolók között aránylag több az allergiás?
(5 pont)
C. 981. Egy hajóskapitány naplójában a képletet találtuk a látóhatár távolságának meghatározására, de a p helyén lévő szám nem jól olvasható. A képletben d a látóhatár távolságát kilométerekben, h pedig a megfigyelő szemének tengerszint feletti magasságát méterekben jelenti. Határozzuk meg a p értékét úgy, hogy egy jól használható képletet kapjunk. (A Föld sugarát vegyük 6370 km-nek.)
(5 pont)
C. 982. Bizonyítsuk be, hogy 52008+4 összetett szám.
(5 pont)
C. 983. Szerkesszük meg az ABCD négyszöget, ha adott a BD egyenes; valamint az A pontból a CD, a B pontból a DA, a C pontból az AB és a D pontból a BC egyenesre bocsátott merőleges talppontja. (A diszkussziótól eltekintünk.)
(5 pont)
C. 984. Egy pozitív számokból álló számtani sorozat nem feltétlenül egymást követő tagja a, b és c. Tudjuk, hogy
Adjuk meg a sorozat differenciáját.
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2009. április 15-én LEJÁRT. |
B. 4162. Egy 30 fős osztály tagjai között kiosztunk 60 darab csokit úgy, hogy mindenki kap csokit, de senki sem kap 31 darabot. Bizonyítsuk be, hogy - mielőtt még bárki is fogyasztott volna a csokikból - kiválasztható az osztályból egy olyan csoport, akiknél összesen pontosan 30 db csoki van.
(4 pont)
B. 4163. 5×10×20 cm élhosszúságú téglákból hézagmentesen felépítünk egy téglatestet. Igazoljuk, hogy ugyanezt úgy is felépíthetjük ezekből a téglákból, hogy azonos hosszúságú éleik mind párhuzamosak legyenek.
(4 pont)
B. 4164. Igazoljuk, hogy ha öt szakasz közül bármelyik háromból háromszög szerkeszthető, akkor létezik három olyan is köztük, amelyekből hegyesszögű háromszög szerkeszthető.
(3 pont)
B. 4165. Egy konvex ABCD négyszög átlóinak metszéspontja O. Bizonyítsuk be, hogy az AB2+BC2+CD2+DA2=2(AO2+BO2+CO2+DO2) összefüggés pontosan akkor áll fenn, ha az AC és BD átlók merőlegesek, vagy ha egyiküknek a felezőpontja O.
Kvant
(3 pont)
B. 4166. Szerkesszünk az ABC háromszög BC oldalán olyan D pontot, amelyre az ABD és az ACD háromszögek beírt körei az AD egyenesen érintik egymást.
(3 pont)
B. 4167. Egy n pozitív egészre jelölje f(n) az n tízes számrendszerbeli alakjának a megfordításával kapható számot. (Tehát f(2500)=52, f(1456)=6541.) Keressük meg azokat a pozitív egész k számokat, amelyekre teljesül, hogy tetszőleges n többszörösükre k az f(n) számnak is osztója.
(5 pont)
B. 4168. Az ABC háromszög beírt körének középpontja K, az AB oldal felezőpontja F, a hozzáírt kör AB oldalon lévő érintési pontja G. Bizonyítsuk be, hogy a CG és KF egyenesek párhuzamosak.
(4 pont)
B. 4169. Igazoljuk, hogy ha a, b, c páronként különböző pozitív egészek, akkor
S=(42a+43b+43c)3+(43a+42b+43c)3+(43a+43b+42c)3
-3(42a+43b+43c)(43a+42b+43c)(43a+43b+42c)
osztható 128-cal, de nem teljes 2-hatvány.
Javasolta: Nagy Donát
(5 pont)
B. 4170. Egy sík az ABCD tetraéder AB, BC, CD, illetve AD éleit rendre a K, L, M és N pontokban metszi. Igazoljuk, hogy
(5 pont)
B. 4171. Egy baktérium minden másodpercben p valószínűséggel elpusztul, 1-p valószínűséggel pedig osztódik két ugyanolyan baktériummá (a leszármazottak egymástól függetlenül pusztulnak el, vagy osztódnak). Mekkora annak a valószínűsége, hogy a baktérium kihal?
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2009. április 15-én LEJÁRT. |
A. 476. Legyen n 3 páratlan egész szám, és legyen
3 páratlan egész szám, és legyen a modulo n maradékosztályok halmaza. Nevezzük holland halmaznak azokat a nemüres B
 A részhalmazokat, amikre bármely a
A részhalmazokat, amikre bármely a A és b
A és b B esetén b+a és b-a közül legalább az egyik B-ben van. Fejezzük ki n függvényében a legkisebb méretű holland halmaz elemszámát.
B esetén b+a és b-a közül legalább az egyik B-ben van. Fejezzük ki n függvényében a legkisebb méretű holland halmaz elemszámát.
Javasolta: Gerhard Woeginger (Amszterdam)
(5 pont)
A. 477. Tegyük fel, hogy a 2n pontú G teljes gráf S1,...,Sk részgráfjaira teljesülnek a következők:
(a) Mindegyik Si teljes páros gráf;
(b) G minden egyes éle páratlan sok Si-ben szerepel.
Mutassuk meg, hogy k n.
n.
(5 pont)
A. 478. Bizonyítsuk be, hogy ha pozitív számok és
, akkor
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

