A KöMaL 2009. májusi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2009. június 15-én LEJÁRT. |
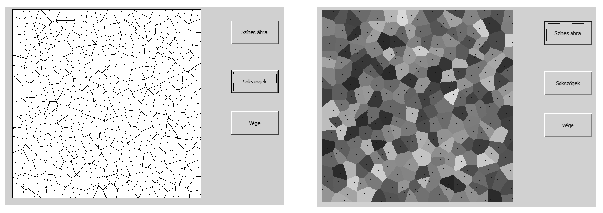
I. 214. Legyen egy négyzetben N darab pontunk valamilyen elrendezésben. Minden pont köré meghatározható egy olyan sokszög, amelynek belső pontjai közelebb vannak a kérdéses ponthoz, mint bármely másik ponthoz. Ezek a sokszögek konvexek és folytonosan töltik ki a négyzetet.
Készítsünk programot, amely egy M×M-es (10 M
M 600) négyzetben véletlenszerűen elhelyez N darab (2
600) négyzetben véletlenszerűen elhelyez N darab (2 M
M 150) pontot, majd határozzuk meg grafikusan a sokszög oldalait, illetve színezzük ki a pontok körüli sokszögeket más-más véletlen színnel. A megjelenítés során a pontokat is rajzoljuk ki.
150) pontot, majd határozzuk meg grafikusan a sokszög oldalait, illetve színezzük ki a pontok körüli sokszögeket más-más véletlen színnel. A megjelenítés során a pontokat is rajzoljuk ki.
Lehetséges eredmények:
Beküldendő a program forráskódja (i214.pas, i214.cpp, ...), valamint a program rövid dokumentációja (i214.txt, i214.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
I. 215. Adott néhány kupac kavics. Minden lépésben az összes kupacból elveszünk egy kavicsot és ezekből egy új kupacot képzünk. A kupacok sorrendje nem számít.
Például:

A lépéseket addig ismételgetjük, amíg meg nem unjuk. Mivel véges a kavicsok száma, így előbb-utóbb a kavicsok eloszlása a kupacokban ciklikussá válik.
Készítsünk táblázatot, amelynek A1:Y1 tartományának első néhány cellájába bejegyezhetők a kupacok kavicsszámai. Az alatta lévő 100 sor mutassa egy-egy újabb lépés után az állapotot úgy, hogy az adott soron belül a kupacok méret szerint csökkenő sorrendben helyezkedjenek el.
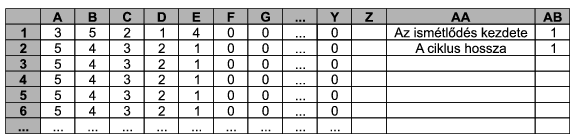
Az AB1 cellában szerepeljen, hogy hányadik lépésben kezdődik az ismétlődés, az AB2-ben pedig adjuk meg, hogy mi a ciklus hossza. Az összes kavics száma nem lehet több mint 25 (ennek ellenőrzése nem része a feladatnak). A megoldás során makró, illetve saját függvény nem használható.
Beküldendő a táblázat (i215.xls, i215.ods, ...), valamint egy rövid dokumentáció (i215.txt, i215.pdf, ...), amely tartalmazza a megoldás rövid leírását és a használt program nevét.
(A probléma azonos a januárban kitűzött I. 202. feladatéval, de most más eszközzel kell megoldani.)
(10 pont)
I. 216. A márciusi számban már megismerkedtünk a ,,MasterMind'' játékkal. Barátunk - elmondása szerint - a következő egyszerű algoritmust használva játszik: a lehetséges tippek lexikografikusan rendezett listájából mindig a legelsőt választja. Annak kiderítésére, hogy valóban ezt a módszert követi-e, írjunk egy programot, amely bármely kitalálandó sorozatra megadja a szükséges tippek számát és a tippek sorrendjét.
A program a standard bemeneten egyetlen sort várjon, a kigondolt karaktersorozatot (szóközök nélkül); a választ a standard kimenetre írja, n lépésben kitalálható feladvány esetén n+1 sorba.
Például, ha a kigondolt jelsorozat ,,DADA'', akkor a kimenet:

Beküldendő a program forráskódja (i216.pas, i216.cpp, ...) valamint a program dokumentációja (i216.txt, i216.pdf, ...), amely megadja, hogy a forrásállomány melyik fejlesztőkörnyezetben fordítható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2009. június 15-én LEJÁRT. |
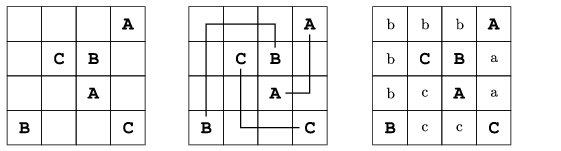
S. 45. Rejtvénylapokban sűrűn előfordul az ún. ,,összekötögetős'' feladat, amelyben egy N×N-es négyzetháló bizonyos mezőiben található azonos betűket kell összekötni úgy, hogy ezek az összekötő vonalak nem metszik és nem is fedik át egymást. Készítsünk programot, amely egy legföljebb 20×20-as négyzethálóban megadja az összes betűpár megfelelő összekötését, ha lehetséges, különben meghatároz egy olyan összeköttetés rendszert, amelyben a lehető legtöbb betűpár szabályosan össze van kötve.
A program a négyzetháló leírását az első parancssori argumentumaként megadott szöveges állományból olvassa. Egy N×N-es négyzetháló esetén a bemeneti állomány N sorból áll, mely sorok mindegyikében N karakter található. Az összekötendő betűk az angol ABC nagybetűi (legföljebb 25), az üres mezők helyén egy szóköz található.
A program a második parancssori argumentumaként megadott szöveges állományba írja a kitöltött táblázatot, amelyben az összeköttetést a nagybetűk között a velük azonos kisbetűk mutatják. Amennyiben az összeköttetés nem teljesen oldható meg, például k betűpár már nem köthető össze, úgy a standard kimenetre írjuk ki a ,,k betűpár összekötése nem sikerült'' szöveget, és a kimeneti állomány csak egy olyan részben kitöltött táblázatot tartalmazzon, ahol a lehető legtöbb betűpár van összekötve.
Beküldendő a program forráskódja (s45.pas, s45.cpp, ...) valamint a program dokumentációja (s45.txt, s45.pdf, ...), amely vázlatosan leírja a megoldás menetét és megadja, hogy a forrásállomány melyik fejlesztőkörnyezetben fordítható.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

