KöMaL Problems in Physics, September 2009
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on October 12, 2009. |
M. 298. Measure how long it takes for an ice cube, made of tap water, to melt if it is in a glass of tap water, which is at room temperature, and if it is in a glass of salt water (saline water), which has the same amount as the glass of tap water and also it is at the same room temperature. Repeat the measurements such that a small weight is frozen into the ice cube, and the cube is completely submerged in both the tap water and the saline water. It is worth dying the cubes with some food colour.
(6 pont)
 |
Problems with sign 'P'Deadline expired on October 12, 2009. |
P. 4174. If the sheets of two exercise books, facing each other, are shuffled into each other, and then the two exercise books are pressed together with two fingers, then even an adult is unable to pull the two exercise books apart. What is the reason for this phenomenon?
(3 pont)
solution (in Hungarian), statistics
P. 4175. Which of the points, marked by A, B, C, D, of the circuit shown in the figure, are at the same potential. Between which two points is the potential difference the greatest?
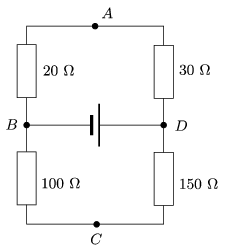
(3 pont)
solution (in Hungarian), statistics
P. 4176. A child sitting on a sleigh slides along an inclined plane, which has an angle of elevation of 10o. There is a small forward wind which exerts a force of 10.5 N on the child in the direction of the motion. The total mass of the child and the sleigh is 65 kg, and the coefficient of kinetic friction between the sleigh and the snow is 0.15.
a) If the sleigh starts from rest swat will the final speed of the sleigh be at the end of the 125 m long inclined plane?
b) How long does it take for the sleigh to reach the bottom of the inclined plane?
(4 pont)
solution (in Hungarian), statistics
P. 4177. A uniform rod of mass m=0.5 kg and of length 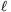 =80 cm is hanged with two threads. What will the acceleration of point A and the tension in the left thread be right after cutting the thread on the right?
=80 cm is hanged with two threads. What will the acceleration of point A and the tension in the left thread be right after cutting the thread on the right?
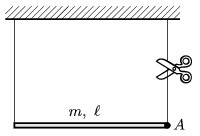
(4 pont)
solution (in Hungarian), statistics
P. 4178. A piece of chocolate is dropped into a glass of soda water. The density of the chocolate is 1,2 g/cm3 and its volume is 2 cm3. Carbon-dioxide bubbles begin to stick to the surface of the chocolate. What is the least total volume of the bubbles when the piece of chocolate begins to ascend?
(4 pont)
solution (in Hungarian), statistics
P. 4179. Determine the ratio of the specific heat capacity of the mixture of 20 g Helium and 8 g Hydrogen at constant pressure to the specific heat capacity of the same gas at constant volume.
(4 pont)
solution (in Hungarian), statistics
P. 4180. A point-like body of mass m and of charge Q is initially at rest on the horizontal tabletop as shown in the figure and is given a v0 vertical, upward speed. There is a horizontal E electric field exerted on the object. With what speed does the object hit the table when it falls back, and what is the distance between the starting point and the point where it hits the table?
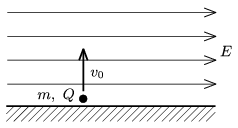
(4 pont)
solution (in Hungarian), statistics
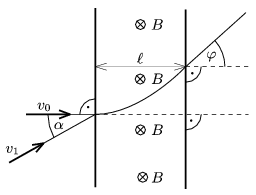
P. 4181. The width of the uniform magnetic field, shown in the figure, is 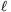 =5 cm, the induction of the field is B=0.167 T. A proton enters into the field perpendicularly to the field lines, and after passing the magnetic field it is deflected by an angle of
=5 cm, the induction of the field is B=0.167 T. A proton enters into the field perpendicularly to the field lines, and after passing the magnetic field it is deflected by an angle of 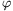 =30o.
=30o.
a) Determine the speed v0 of the proton and the time while it passes the magnetic field.
b) What voltage is to be applied in order to stop the proton in a distance of s=10 cm, and how long does it take to stop the proton?
c) Suppose that another proton enters into the magnetic field at a speed of v1=2.106 m/s, and at the angle 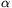 , shown in the figure. What is the least angle
, shown in the figure. What is the least angle 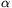 , if the particle bounces back from the magnetic wall?
, if the particle bounces back from the magnetic wall?
(5 pont)
solution (in Hungarian), statistics
P. 4182. A pointlike discharge lamp of power 5 W emits monochromatic light of wavelength 425 nm. The cathode of a photocell is placed 1 m from the light source, perpendicularly to the light rays. The radius of the cathode is 0.5 cm and the work function of its material is 2.10-19 J. A capacitor of capacitance 2 nF is connected to the anode and the cathode of the photocell.
a) What is the energy of one photon emitted by the discharge lamp? How many photons hits the cathode of the photocell in each second?
b) What is the maximum of the speed of the electrons which leaves the cathode?
c) What will the voltage of the capacitor be?
(5 pont)
solution (in Hungarian), statistics
P. 4183. The halflife of the radioactive isotope of lead, whose atomic mass number is 214, is 26.8 minutes. How long has it been decaying if only one-thousandth of the original atoms are present in the sample?
(4 pont)
Upload your solutions above.
