KöMaL Problems in Mathematics, September 2009
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on October 12, 2009. |
K. 211. We have five peaches of different sizes and three apples of different sizes. We need to divide them into two packs of four fruits, each of which contains an apple. In how many different ways can we do that? (Two divisions are considered different if the fruits of different types and sizes are not divided in the same way.)
(6 pont)
solution (in Hungarian), statistics
K. 212. Four football teams organize a championship. Every team plays every other team once. The winning teams scores 3 points, the losing team scores 0 points and each team scores 1 point if there is a draw. The Albatrosses did not lose any game and won the tournament. The Black Sheep came out second. They did not have any draws. The third place went to the Cheerful Devils who did not win any game. The Dragonflies were in the fourth place. (In the case of equal scores, the order of teams is determined by the game played against each other. If it is a draw, a tie is declared.) Show that under the given conditions the scores of the four teams were different. List who was the winner in which game and which games ended with a draw. Justify your answers.
(6 pont)
solution (in Hungarian), statistics
K. 213. A rectangle is cut into nine pieces with lines parallel to its sides (see the Figure.). The area in cm2 is written in each field. Find the area of the field marked x.
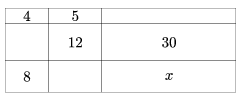
(6 pont)
solution (in Hungarian), statistics
K. 214. In the interior of a square ABCD a point P is marked such that the triangles PAB and PCD are congruent. Determine the set (locus) of such points P.
(6 pont)
solution (in Hungarian), statistics
K. 215. The fields of a 3×3 table are filled in with different digits, such that the three-digit numbers read left to right in the rows and down the columns are all divisible by six. How many of them will be divisible by five?
(6 pont)
solution (in Hungarian), statistics
K. 216. Prove that a median of a triangle is always shorter than the arithmetic mean of the adjacent sides.
(6 pont)
 |
Problems with sign 'C'Deadline expired on October 12, 2009. |
C. 995. Show that the simultaneous equations x-y+2z=0, -2x+y-2z=-2, 2x+cy+3z=1 have a solution that is independent of the value of the parameter c.
(5 pont)
solution (in Hungarian), statistics
C. 996. Given six different points in the plane such that at least three of any four are collinear. Prove that at least five of the points lie on the same line.
(5 pont)
solution (in Hungarian), statistics
C. 997. Prove that every fourth term of the Fibonacci sequence is divisible by three. (In the Fibonacci sequence, a1=1, a2=1 and an=an-1+an-2 for all , n
 3.)
3.)
(5 pont)
solution (in Hungarian), statistics
C. 998. The points A, B, C and D lie on a line in this order, and AB=BC. Draw perpendiculars to AD at B and C. The perpendicular drawn at B intersects the circle of diameter AD at P and Q. The perpendicular drawn at C intersects the circle of diameter BD at K and L. Show that the centre of the circle passing through points P, K, L and Q is point B.
(5 pont)
solution (in Hungarian), statistics
C. 999. A coin is tossed four times. Then it is tossed again, the number of times a head was obtained in the first four tosses. What is the probability of getting at least 5 heads altogether?
(5 pont)
 |
Problems with sign 'B'Deadline expired on October 12, 2009. |
B. 4192. The numbers 1 to 2009 are written on a sheet of paper. Then the double of each number is also written on it. Finally, all those numbers are erased that occur twice. This procedure is repeated in the following way: In the ith step, i times the numbers are written on the sheet, and all those numbers are erased that occur twice. How many numbers will be on the sheet after 2009 steps?
(4 pont)
solution (in Hungarian), statistics
B. 4193. Out of a set of one million lottery tickets issued with numbers 000000 to 999999, a group of friends bought all tickets that they considered ``lucky'', that is the ones with numbers , such that af+be+cd=100. Prove that the sum of the numbers of the remaining tickets is divisible by 1001.
(4 pont)
solution (in Hungarian), statistics
B. 4194. The angle at vertex C of a triangle is a right angle. The angle bisector and altitude drawn from C intersect the circumscribed circle at D and E, respectively. The not shorter leg of the triangle is b. Show that the length of the broken line CDE is .
(4 pont)
solution (in Hungarian), statistics
B. 4195. The length of the altitudes of a triangle are 10, 12 and 15. How long are the sides?
Suggested by J. Pataki, Budapest
(3 pont)
solution (in Hungarian), statistics
B. 4196. Let n be a positive integer. What is the first digit after the decimal point in the number ?
(3 pont)
solution (in Hungarian), statistics
B. 4197. Prove that if the sides of a triangle satisfy 2b2=a2+c2, then the opposite angles satisfy 2cot  =cot
=cot  +cot
+cot 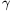 .
.
(3 pont)
solution (in Hungarian), statistics
B. 4198. The midlines are drawn on the base of a regular tetrahedron. The midpoint of each midline is connected to the vertices of the face whose plane is parallel to the midline. Consider the volume of the intersection of the three tetrahedra obtained. What fraction of the volume of the original tetrahedron is it?
(4 pont)
solution (in Hungarian), statistics
B. 4199. A triangulation of a finite point set A in the plane is defined as a partition of its convex hull into triangles such that the vertices of each triangle are elements of A, and no triangle contains any element of A apart from its vertices. Prove that all triangulations of a set A consist of the same number of triangles.
(4 pont)
solution (in Hungarian), statistics
B. 4200. For a finite point set \(\displaystyle A\) in the plane, let \(\displaystyle v(A)\) denote the number of triangles in a triangulation of set \(\displaystyle A\), and let \(\displaystyle A+A=\{x+y\mid x,y\in A\}\), where the sum of two points is defined as the point whose position vector is the sum of the position vectors of the terms. Prove that \(\displaystyle v(A+A)\ge 4v(A)\).
Suggested by I. Ruzsa, Budapest
(5 pont)
solution (in Hungarian), statistics
B. 4201. Prove that the inequality is true for all positive numbers a, b, c.
(5 pont)
 |
Problems with sign 'A'Deadline expired on November 10, 2009. |
A. 485. Let ABCD be a tetrahedron with circumcenter O. Suppose that the points P, Q and R are interior points of the edges AB, AC and AD, respectively. Let K, L, M and N be the centroids of the triangles PQD, PRC, QRB and PQR, respectively. Prove that if the plane PQR is tangent to the sphere KLMN then OP=OQ=OR.
(5 pont)
A. 486. Denote by 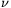 (n) the exponent of 2 in the prime factorization of n!. Show that for arbitrary positive integers a and m there exists an integer n>1 for which
(n) the exponent of 2 in the prime factorization of n!. Show that for arbitrary positive integers a and m there exists an integer n>1 for which .
(5 pont)
A. 487. Let x, y, z be positive numbers satisfying xyz 1. Prove that
1. Prove that .
Proposed by Tuan Le, Anaheim, California, USA
(5 pont)
Upload your solutions above.
