A KöMaL 2009. szeptemberi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
K-jelű feladatokA beküldési határidő 2009. október 12-én LEJÁRT. |
K. 211. Öt különböző nagyságú barackunk, és három különböző nagyságú almánk van. Két csomagot kell készítenünk belőlük úgy, hogy mindkét csomagban négy-négy gyümölcs legyen, melyek egyike alma. Hányféleképpen tehetjük ezt meg? (Két csomagolás akkor különböző, ha nem ugyanúgy osztottuk szét a különböző fajtájú és méretű gyümölcsöket.)
(6 pont)
K. 212. Négy csapat körmérkőzéses labdarúgó-bajnokságon vett részt, minden csapat minden csapattal egyszer játszott. A mérkőzéseken a döntetlenért 1 pont, a győzelemért 3 pont, a vereségért 0 pont járt. A bajnokságot az Albatroszok nyerték, akik egyszer sem kaptak ki, a második helyezést a Betyárok szerezték meg, akik nem játszottak döntetlent, harmadikok pedig a Csíkos ördögök lettek, akik nem nyertek egy mérkőzést sem. Negyedik helyen a Dongók csapata végzett. (A csapatok sorrendjét pontszámegyenlőség esetén az egymás elleni eredmény dönti el, ha ez döntetlen, akkor holtversenyt hirdetnek.) Mutassuk meg, hogy a versenyben a megadott feltételek mellett a négy csapat összpontszáma különböző volt. Adjuk meg, hogy melyik mérkőzésen ki nyert, illetve melyiken volt döntetlen. Válaszunkat indokoljuk.
(6 pont)
K. 213. Egy téglalapot az oldalaival párhuzamos vágásokkal kilenc darabra vágtunk. Az egyes darabokba beleírtuk a területüket cm2-ben kifejezve. Mennyi az x-szel jelölt darab területe?
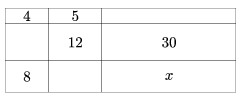
(6 pont)
K. 214. Az ABCD négyzet belsejében úgy vesszük fel a P pontot, hogy a PAB és a PCD háromszögek egybevágók legyenek. Mi a megfelelő P pontok halmaza (mértani helye)?
(6 pont)
K. 215. Egy 3×3-as táblázatba különböző számjegyeket írtunk úgy, hogy a sorokból balról jobbra és az oszlopokból felülről lefelé (tízes számrendszerben) kiolvasható háromjegyű számok mind oszthatók 6-tal. Hány szám lesz ezek közül osztható 5-tel?
(6 pont)
K. 216. Bizonyítsuk be, hogy egy tetszőleges háromszög súlyvonalának hossza kisebb az őt közrefogó háromszögoldalak számtani közepénél.
(6 pont)
 |
C-jelű feladatokA beküldési határidő 2009. október 12-én LEJÁRT. |
C. 995. Igazoljuk, hogy az
egyenletrendszernek van olyan megoldása, amely nem függ a c paraméter értékétől.
(5 pont)
C. 996. Adott a síkon hat különböző pont úgy, hogy bármely négy kiválasztott pont közül legalább három egy egyenesen van. Bizonyítsuk be, hogy ekkor a pontok közül legalább öt egy egyenesre illeszkedik.
(5 pont)
C. 997. Bizonyítsuk be, hogy a Fibonacci-sorozat minden negyedik tagja osztható 3-mal. (A Fibonacci-sorozatban a1=1, a2=1 és an=an-1+an-2 minden , n
 3 esetén.)
3 esetén.)
(5 pont)
C. 998. Az A, B, C és D pontok ebben a sorrendben egy egyenesre illeszkednek, és AB=BC. Állítsunk B-ben és C-ben az AD-re merőlegest. A B-ben állított merőleges az AD átmérőjű kört P-ben és Q-ban, a C-ben állított merőleges a BD átmérőjű kört a K és L pontokban metszi. Igazoljuk, hogy a P, K, L és Q pontokra illeszkedő kör középpontja B.
(5 pont)
C. 999. Fej vagy írást játszunk a következőképpen: Négyszer dobunk és utána még annyiszor, ahány fej volt az első négy dobás során. Mennyi annak a valószínűsége, hogy összes dobásunk közül legalább 5 fej lesz?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2009. október 12-én LEJÁRT. |
B. 4192. Egy papírlapra felírtuk a számokat 1-től 2009-ig. A második lépésben mindegyik szám kétszeresét is felírtuk a papírra, majd kiradíroztuk azokat a számokat, amelyek kétszer is szerepeltek. Ezt a lépést ismételgetjük olyan módon, hogy az i-edik lépésben az számok mindegyikének i-szeresét is felírjuk a papírra, majd kiradírozzuk azokat a számokat, amelyek kétszer is szerepelnek. Hány szám lesz a papírlapon a 2009. lépés után?
(4 pont)
B. 4193. Egymillió darab kiadott sorsjegyből, melyek sorszáma 000000-tól 999999-ig változik, egy baráti társaság megvásárolta az összes olyan -- általuk szerencsésnek mondott -- sorsjegyet, amelyek sorszámára teljesül, hogy
af+be+cd=100.
Bizonyítsuk be, hogy a megmaradt sorsjegyek sorszámainak összege osztható 1001-gyel.
(4 pont)
B. 4194. Egy háromszög C csúcsánál levő szöge derékszög. A C-hez tartozó szögfelező és magasság a köré írt kört a D, illetve az E pontban metszi. A háromszög nem rövidebbik befogója b. Igazoljuk, hogy a CDE töröttvonal hossza .
(4 pont)
B. 4195. Egy háromszög magasságainak hossza 10, 12 és 15. Mekkorák az oldalai?
Javasolta: Pataki János (Budapest)
(3 pont)
B. 4196. Legyen n pozitív egész. Határozzuk meg a
szám tizedesvessző utáni első számjegyét.
(3 pont)
B. 4197. Igazoljuk, hogy ha egy háromszög oldalaira 2b2=a2+c2 teljesül, akkor a háromszög megfelelő szögeire
(3 pont)
B. 4198. Egy szabályos tetraéder alaplapján megrajzoljuk a középvonalakat. Minden középvonal felezőpontját összekötjük a középvonallal párhuzamos oldallap csúcspontjaival. Hányadrésze az így kapott három tetraéder közös részének térfogata a tetraéder térfogatának?
(4 pont)
B. 4199. Egy síkbeli A véges ponthalmaz háromszögelése alatt A konvex burkának olyan egymásba nem nyúló háromszögekre történő felbontását értjük, amelyben minden egyes háromszög csúcsai A pontjai közül kerülnek ki, és a csúcspontjai kivételével egy háromszög sem tartalmazza A-nak egyetlen további pontját sem. Igazoljuk, hogy az A halmaz bármely két háromszögelése ugyanannyi háromszöget tartalmaz.
(4 pont)
B. 4200. Tetszőleges síkbeli \(\displaystyle A\) véges ponthalmazra jelölje \(\displaystyle v(A)\) az \(\displaystyle A\) halmaz egy háromszögelésében található háromszögek számát, és legyen
\(\displaystyle A+A=\{x+y\mid x,y\in A\}, \)
ahol két pont összege alatt azt a pontot értjük, amelynek helyvektora az összeadandók helyvektorának összege. Bizonyítsuk be, hogy
\(\displaystyle v(A+A)\ge 4v(A). \)
Javasolta: Ruzsa Imre (Budapest)
(5 pont)
B. 4201. Igazoljuk, hogy tetszőleges a, b, c pozitív számokra fennáll a következő egyenlőtlenség:
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2009. november 10-én LEJÁRT. |
A. 485. Legyen az ABCD tetraéder körülírt gömbjének középpontja O. Tegyük fel, hogy P, Q, illetve R az AB, AC, illetve AD élek egy-egy belső pontja. Legyenek K, L, M, illetve N a PQD, PRC, QRB, illetve PQR háromszögek súlypontjai. Bizonyítsuk be, hogy ha a PQR sík érinti a KLMN gömböt, akkor OP=OQ=OR.
(5 pont)
A. 486. Jelöljük 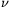 (n)-nel a 2 kitevőjét az n! prímtényezős felbontásában. Mutassuk meg, hogy tetszőleges a és m pozitív egészekhez létezik olyan n>1 egész szám, amire
(n)-nel a 2 kitevőjét az n! prímtényezős felbontásában. Mutassuk meg, hogy tetszőleges a és m pozitív egészekhez létezik olyan n>1 egész szám, amire .
(5 pont)
A. 487. Legyenek \(\displaystyle x\), \(\displaystyle y\), \(\displaystyle z\) pozitív számok, amelyekre \(\displaystyle xyz\ge 1\). Igazoljuk, hogy
\(\displaystyle \frac{x}{x^3+y^2+z}+ \frac{y}{y^3+z^2+x}+ \frac{z}{z^3+x^2+y}\le 1. \)
Javasolta: Tuan Le (Anaheim, Kalifornia, USA)
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

