KöMaL Problems in Informatics, October 2009
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on November 10, 2009. |
I. 220. Due to the varying hardness of the rocks, a tunnel boring machine could not exactly drive a horizontal tunnel as calculated. After the tunnel has been excavated, they measured at each meter the relative height of the floor and ceiling of the tunnel, compared to the originally planned base level. (Therefore, the base level has relative height 0 cm.)
In the first line of the file magassag.txt, downloadable from our webpage, you will find the number of measurements N (3 N
N 1000), then, in the following N lines the relative heights (in centimeters, between -100 and 600) of the floor and ceiling of the tunnel are found, compared to the base level.
1000), then, in the following N lines the relative heights (in centimeters, between -100 and 600) of the floor and ceiling of the tunnel are found, compared to the base level.
|
You can interpret the data in the example as follows:
* data for 95 measurement points are stored;
* at the first measurement point, the boring machine achieved the exact lower height, and it created the upper height of the tunnel 511 cm above base level;
* at the third measurement point, for example, the machine dug 3 cm below the base level and created the tunnel ceiling 507 cm above the base level.
You should create a program alagut to solve the following tasks. (If a task requires displaying some data, the number of the actual task, e.g. Task #3, should also be written on the screen.)
1. Read data from the file magassag.txt and solve the following questions. If the file can not be read, use the first 10 lines of the source as input to solve the tasks.
2. Display on the screen the minimal inner height of the tunnel (understood to be the difference between ceiling height minus floor height relative to the base level).
3. In order to make the tunnel more regular, first the ceiling is made smoother. Beginning with the second measurement point and ending with the last but one, each ceiling height is averaged with the previous and succeeding ceiling heights. This average of 3 measurements is then rounded up to the nearest whole cm. If the average is higher than the actual ceiling height at that point, then the ceiling is excavated further, up to the average height. (If the average is not higher than the actual ceiling height, nothing happens.) Excavated soil drops down vertically to the floor (exactly at the actual measurement point), and increases the floor level (with exactly the same number of centimeters). When averaging ceiling heights at the next measurement point, this possibly modified new value will be used. You should display how many cm were excavated (provided that this number is greater than zero) from the ceiling at which measurement point. You should use a format like ``At measurement point #3, 1cm''.
4. Express in centimeters how much soil surplus or deficit is present altogether on the floor of the tunnel, relative to the base level.
5. In the next phase a road grader goes through the tunnel (in the original direction). This machine removes soil above the base level. The machine also stores excavated soil and takes it away. If the machine has enough stored soil in its containers, it spreads soil evenly where floor level is too low. If the machine carries no more soil, it leaves lower regions intact and continues with grading at the next measurement point, if necessary. The road grader is empty when it starts. You should write into file talaj.txt the floor level at each measurement point after the machine went through the tunnel once.
6. Display on the screen the beginning and ending measurement points corresponding to the lowest floor level (after the earthwork in the previous steps is done). If there are more than one pit with the same deepest depth, display only the first one. (The boundary of a pit is the first and last negative value.) If there are no negative values at all, display ``The floor is smooth.''
The source code (i220.pas, i220.cpp, ...) together with a short documentation (i220.txt, i220.pdf, ...) -- also describing which developer environment to use for compiling, further a brief description of your solution -- should be submitted in a compressed file (i220.zip). 3. 2.
(10 pont)
solution (in Hungarian), statistics
I. 221. Peter and Paul are jealous twins. They very carefully share everything until both of them get exactly the same amount. This year they were given 25 birthday presents with total value less than 1000 EUR. You have to figure out whether these presents can be shared among the twins such that both get the same value.
You should solve this task with a spreadsheet application. Cells B3:Z3 contain the value of the presents, being integers. Your answer should appear in cell A1. You should not use macros or user defined functions.
The spreadsheet (i221.xls, i221.ods, ...) together with a short documentation (i221.txt, i221.pdf, ...) -- also describing the name and version number of the spreadsheet application, further a brief description of your solution -- should be submitted in a compressed file (i221.zip).
(10 pont)
solution (in Hungarian), statistics
I. 222. Draw the topology of the computer network of your school. The figure should contain at least one computer room, machines available for students, some computers in a classroom and in a lab, further, some routers, switches and other network devices, finally, the Internet connection. The figure should contain the main characteristics of these devices in the network, but the figure should not be overcrowded. Data for this exercise can be obtained from your school system administrator or teacher of computer science. To solve the task, you should use the freely downloadable program Dia, http://live.gnome.org/Dia.
You should submit the network topology (i222.dia) and also a PDF version of this file (i222.pdf) in a compressed file (i222.zip), also containing the version number of the program and the operating system.
(10 pont)
 |
Problems with sign 'S'Deadline expired on November 10, 2009. |
S. 47. Prepare your program to evaluate cells of a spreadsheet, if some simple formulae and certain numerical values are given. The 25 columns of the worksheet are denoted by capital letters of the English alphabet from A to Y, further, there are 100 rows numbered from 1 to 100. Each cell can contain an integer, a real number (given by simple operations), the four basic operations or cell references. The expressions are syntactically correct, they may contain absolute, relative, or mixed cell references. However, cells contain neither exponentials, nor parentheses.
The input file of your program to be read is given as the first argument in the command line.
Only cells with nonzero values should be read (all other cells contain 0). Each line of the input file describes either a single cell, or a group of cells of a rectangular domain. The name of the output file is given as the second command line argument. The output file should contain the evaluated cells: each value should be an integer or a real number rounded to 2 decimal places. The output file should contain only nonzero values of the evaluated spreadsheet, in CSV format, with each line and value separated by semicolons.
In the first example, be01.txt is a sample input, while ki01.csv is the corresponding output.
In the input file, two cells have nonzero values (one integer and one real number). In a third cell we have also computed their arithmetic mean, and added 20, then 0. The third row of the output file, as well as the first cell of the fourth row is empty.
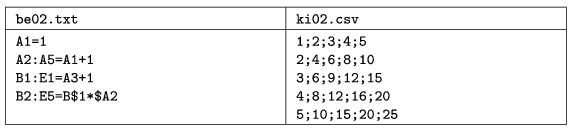
In the second example, the formula in cells A2:A5 with relative reference adds 1 to the value of the cell left to the actual cell and being in the same row, so this formula literally appears in the top left cell of the domain. The same applies to formulae in B2:E5 with mixed reference.
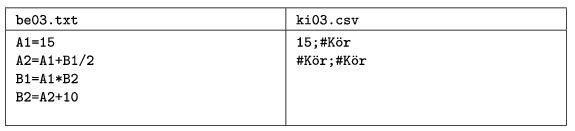
The third example contains some circular references. These values can not be computed and should be denoted by #Kör. Division by zero should be indicated by #NulOszt.
The source code and project files of your solution (without the .exe file or any other auxiliary files generated by the compiler) together with a brief documentation of your solution should be submitted in a compressed file (s47.zip).
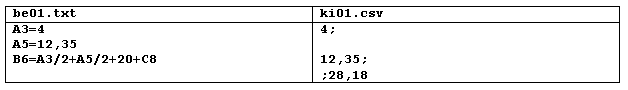
(10 pont)
$Var(Body)
Upload your solutions above
