KöMaL Problems in Physics, February 2010
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on March 10, 2010. |
M. 303. Place an inclined plane to the rim of the table and let a paper cylinder roll down along the incline. Observe the path of the cylinder flying off the table. Investigate what the distance between the table and position where the cylinder reaches the ground depends on, and how it depends.
(6 pont)
 |
Problems with sign 'P'Deadline expired on March 10, 2010. |
P. 4224. Two bulbs, rated at 230 V 40 W and 230 V 60 W, are connected in series to a voltage supply of 230 V. Which bulb will be brighter and why?
(3 pont)
solution (in Hungarian), statistics
P. 4225. Two balls are started at the same time, one of them starts from rest at the top of the inclined plane, the angle of inclination is  , and the other is projected from point O, and they reach point P at the same time. At what angle does the second ball have to be projected?
, and the other is projected from point O, and they reach point P at the same time. At what angle does the second ball have to be projected?
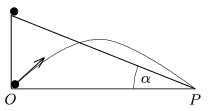
(4 pont)
solution (in Hungarian), statistics
P. 4226. What happens to the compass placed as shown in the figure, if a) the switch is
turned on,
b) then keeping the switch on, the the wiper of the variable resistor is moved in the direction shown by the arrow.
c) then, still keeping the switch on, the bar of soft iron is pushed into the coil.
d) finally the switch is turned off.
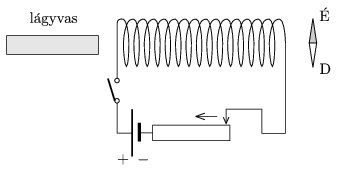
(4 pont)
solution (in Hungarian), statistics
P. 4227. The density of an imaginary planet is 5.103 kg/m3, its radius is 5000 km. Inside the planet there is an enormous spherical hole, the radius of which is 1000 km, and whose centre is 3000 km from the geometric centre of the planet. What is the acceleration of that meteoroid which at one moment is at a distance of 6000 km from the geometric centre of the planet and the line segment which joins the centre of the planet and the meteoroid makes an angle of 60o with the line segment between the centres of the planet and the hole.
(5 pont)
solution (in Hungarian), statistics
P. 4228. Determine and graph the heat of vaporization of water as a function of temperature between 0 oC and 100 oC. The data that can be used are: the specific heat capacity values of water and water vapour, and the specific latent heat of vaporization of water.
(5 pont)
solution (in Hungarian), statistics
P. 4229. The heating system keeps the temperature of a flat at about 20 oC. Outside the weather is cold and damp: the temperature is 0 oC, and the relative humidity is 95%. What will the relative humidity of the air in the room be after airing the room, when the temperature reaches again the value of 20 oC? Approximately what amount of water must be vaporized in a flat of area 50 m2 and of height 3 m, in order to reach the 50% relative humidity, pleasant for the human mucous membrane.
(5 pont)
solution (in Hungarian), statistics
P. 4230. Uniformly charged square-shaped sheets of sides a and of charge Q, are used to build a cube. What is the electrostatic repelling force exerted on each face of the cube?
(5 pont)
solution (in Hungarian), statistics
P. 4231. Metal pieces of wires, of resistance R are used to build a cube system as shown in the figure. The cubes make a long chain, which can be considered infinite. What is the equivalent resistance between points A and B?
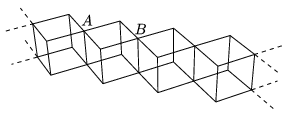
(5 pont)
solution (in Hungarian), statistics
P. 4232. A 2-m long metal rod falls, because of the gravitational pull, but it falls with a constant speed of 50 m/s because its motion is damped. What can the maximum voltage be between the two ends of the rod?
(4 pont)
solution (in Hungarian), statistics
P. 4233. The inside of a half cylinder is silver-coated. The radius of the cylinder is R=6 cm. At a distance of h=4 cm from its symmetry axis there is a narrow beam of light. At what point does this beam of light focused?
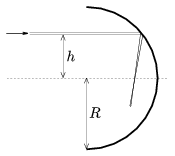
(5 pont)
Upload your solutions above.
