A KöMaL 2010. februári informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2010. március 10-én LEJÁRT. |
I. 232. Az adatokat tartalmazó naplo.txt állomány.
Az internetes csomagkapcsolt kommunikáció üzenetküldő eljárását az alábbi egyszerű modellel vizsgáljuk.
A kommunikációt létrehozó szoftverek a kommunikálók egymásnak szánt üzeneteit szabvány méretű darabokra tördelik, azokat a továbbításhoz szükséges adatokkal egészítik ki. Ezeket, az úgynevezett csomagokat küldik el. A csomagok nem feltétlenül a feladás sorrendjében érkeznek meg a címzetthez.
Az egyes üzenetdarabokat tartalmazó csomag szerkezete a következő:
|
A hálózati modell működését egy rövid teszttel vizsgáljuk, melynek részeként az összes beérkező üzenetdarabot a naplo.txt fájlba rögzítjük.
Például:
naplo.txt
11 3 334 2 verseny||| 2
3 2 417 1 Hatarido:_ 88
11 3 334 1 KoMaL_pont 29
...
Az 1. sor megmutatja, hogy a 11. állomás küldött üzenetet a 3. állomásnak. Az üzenetet a 334-es azonosítóval látta el, amelynek második részét tartalmazza ez a csomag. Mivel a szűrő karakter (|) szerepel, ezért ez az üzenet utolsó darabja.
Készítsünk programot halo néven, amely az alábbi kérdésekre válaszol. Ügyeljünk arra, hogy a program minden helyes tartalmú bemeneti állomány esetén működjön.
Minden részfeladat megoldása előtt írjuk a képernyőre a feladat sorszámát. Ha a felhasználótól kérünk be adatot, jelenítsük meg a képernyőn, hogy milyen értéket várunk (például az 5. feladat esetén: ,, 5. feladat: Adja meg az üzenet szövegét!''). A képernyőn megjelenített üzenetek esetén az ékezetmentes kiírás is elfogadott.
[1.] Olvassuk be a naplo.txt állományban talált adatokat (honlapunkról egy mintaállomány letölhető), s azok felhasználásával oldjuk meg a következő feladatokat. Ha az állományt nem tudja a programmal beolvasni, az első 10 csomaghoz tartozó adatokat jegyezzük be a programba és dolgozzunk azzal.
[2.] Jelenítsük meg a képernyőn, hány csomagot küldött az 4-es állomás az 5-ösnek.
[3.] Írjuk a képernyőre a hibás ellenőrző összeget tartalmazó sorok sorszámát. Az egyes értékeket szóközzel határoljuk. Ha nem volt ilyen, akkor a ,,Nem volt hibás ellenőrző összeg.'' szöveget jelenítsük meg.
[4.] A naplo.txt állomány feldolgozásával állítsuk elő az eredeti üzeneteket. Az eredeti.txt állományba soronként egy-egy üzenetet jegyezzünk be. A fájl tartalmát az alábbi mintának megfelelően alakítsuk ki. (A minta illeszkedik a feladat elején megadott bemenethez.) Az üzeneteket tetszőleges sorrendben megadhatjuk.
eredeti.txt
11 3 334 KoMaL_pontverseny
...
[5.] Bontsunk csomagokra egy üzenetet. A felhasználótól kérjük be az üzenet szövegét, valamint azt, hogy melyik állomástól melyikhez kell eljuttatni. Az elkészített csomagokat soronként írjuk a képernyőre. Biztosítsuk, hogy az üzenet azonosítója ne egyezzen meg a korábbi üzenetek egyikével sem, de egyébként tetszőleges érték lehet.
Beküldendő egy tömörített (i232.zip) állományban a program forráskódja (i232.pas, i232.cpp, ...), valamint a program rövid dokumentációja (i232.txt, i232.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
I. 233. Kincsgyűjtő játékot valósítsunk meg táblázatkezelő program segítségével.
A játéktér 10×10 cellából áll, amelyek közül ötben kincs van. A játéktérben egy robotot vezérelhetünk. A cél, hogy a robottal minél több kincset gyűjtsünk össze. Ha a robot a kincs cellájára lép, akkor azt begyűjtötte. A játékos látja előre a kincseket és feladata, hogy egyetlen vezérlő parancssort adjon a robotnak, amellyel az minél több kincset tudjon begyűjteni.
A robot induló helyzetének koordinátáit két cellában adjuk meg és az, alapértelmezetten, kezdetben lefelé néz. A robot mozgását és irányváltását az A1 cellába írt karaktersorral tudjuk vezérelni. A használható karakterek jelentése:
|
A játéktér celláiba olyan függvényeket írjunk, amelyek kiértékelés utáni eredménye jól felhasználható feltételes formázásra, mintázat állításra, az események megjelenítésére.
A táblázat 5×2 cellájában adjuk meg a kincsek koordinátáit. A kincseket piros színnel és az A1 cella vezérlő karaktersora alapján a robot mozgását fekete színnel jelenítsük meg a játéktérben. A kincs cellájának színét ne változtassuk meg, amikor a robot arra rálép.
Minta a játéktérre:
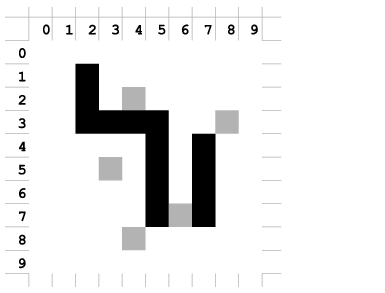
Írjuk ki, hogy egy vezérlő parancssorral hány kincset sikerült begyűjteni.
A robot helyének és irányának számítását másolható függvényekkel oldjuk meg. A játék megvalósítása közben nem szükséges ellenőrizni, hogy a robot kimegy-e a játéktérből. A megoldás során saját függvény vagy makró nem alkalmazható. A számítások, esetleges segédtáblázatok jól áttekinthetők legyenek, semmit ne rejtsünk el.
Beküldendő egy tömörített i233.zip állományban a táblázatkezelő munkafüzet (i233.xls, i233.ods, ...), illetve egy rövid dokumentáció (i233.txt, i233.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziója, valamint a megoldás rövid leírása.
(10 pont)
I. 234. Készítsünk iskolánkat bemutató prezentációt a http://prezi.com címen elérhető eszköz segítségével. A bemutató a szöveg és képek mellett legalább egy videót is tartalmazzon. Az értékelés során a bemutató tartalmasságát és egységességét vesszük figyelembe. A bemutatón a beadási határidőt követően már ne változtassunk.
Beküldendő az i234.pdf dokumentum, amely tartalmazza a bemutató internetes elérhetőségét és a benne szereplő dokumentumok forrását.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2010. március 10-én LEJÁRT. |
S. 51. Egy vállalatnál az informatikai infrastruktúra modernizálásának jegyében ún. ultravékony kliensek bevezetését tervezik: az asztali számítógépeket egy-egy végtelenül egyszerű berendezéssel helyettesítik, melyek feladata mindössze annyi, hogy a billentyűzetről és az egérről érkező bemenetet egy központi szerverre továbbítsák, majd az onnan érkező kimenetet megjelenítsék a képernyőn. A programok futtatását, illetve minden ezzel kapcsolatos számítást valójában a központi szerver végez.
A rendszernek, számos előnye mellett, hátránya, hogy érzékeny a hálózati késleltetésre. Ezért a szervert optimálisan úgy kell elhelyezni, hogy a kliensek szervertől vett késleltetéseinek maximuma minimális legyen.
Írjunk programot, mely meghatározza, hogy a szerver optimális elhelyezése esetén mekkora lesz a hálózati késleltetés a szerver és a tőle legtávolabb eső kliens között. A hálózat fatopológiájú, tehát bármely két csúcs között pontosan egy út vezet. A kliensek a hálózat végpontjaiban (a fa leveleiben) helyezkednek el, a szervert pedig valamely belső csomópontba kell telepíteni.
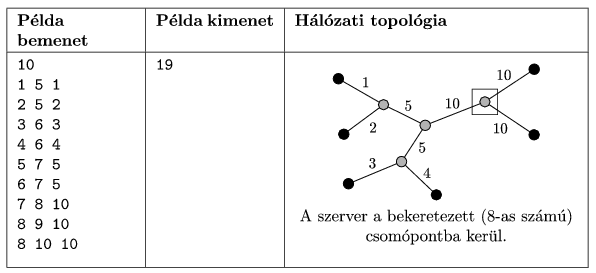
A program a hálózat leírását a standard bemenetről olvassa. A bemenet első sora egyetlen egész számot, a csúcsok számát tartalmazza. Az ezt követő N-1 sor mindegyike három, szóközzel elválasztott egész számot tartalmaz, egy-egy hálózati összekötés végpontjainak Xi és Yi sorszámát (1
 Xi,Yi
Xi,Yi N), illetve az összekötés 0
N), illetve az összekötés 0 Di
Di 1000 késleltetését (a két végpontbeli feldolgozáshoz szükséges idő elhanyagolható).
1000 késleltetését (a két végpontbeli feldolgozáshoz szükséges idő elhanyagolható).
A program a megoldást a standard kimenetre írja, melynek egyetlen sora egyetlen M egész számot tartalmazzon: az optimális szerverelhelyezés esetén a késleltetések maximumát.
A feladathoz kiadott tesztesetek: s51test.zip
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

