A KöMaL 2010. márciusi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2010. április 12-én LEJÁRT. |
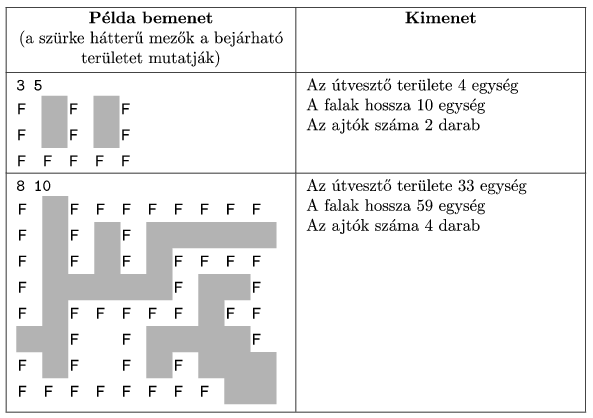
I. 235. Egy bonyolult, útvesztőszerű pincerendszer felmérését kell elvégeznünk. Az alaprajz téglalap alakú; és átjárható, valamint fal mezőkből épül fel. (Csak az éllel való érintkezés számít a mezőknél.) Az átjárható mező 1 egység oldalhosszúságú négyzet.
A pincerendszernek több ajtaja van és elzárt részei is lehetségesek. Előfordulhat olyan terület, amely az egyik ajtón belépve elérhető, de másikon keresztül nem. Az alaprajz minden oldalán legalább egy egység fal van.
Készítsünk programot, amely meghatározza, hogy mekkora területű az útvesztő bejárható része. Határozzuk meg, hogy a bejárható pincerendszernek milyen hosszú összesen a fala és hány ajtaja van.
A program parancssori argumentuma legyen a pincerendszert leíró adatállomány neve. A fájl első sorában szóközzel elválasztva N (3 N
N 1000) a sorok száma, valamint M (3
1000) a sorok száma, valamint M (3 M
M 1000) az oszlopok száma szerepel, és az ezt követő N sorban az alaprajz található. Minden fal mezőt ,,F'', minden átjárható mezőt ,, '' (szóköz) ír le.
1000) az oszlopok száma szerepel, és az ezt követő N sorban az alaprajz található. Minden fal mezőt ,,F'', minden átjárható mezőt ,, '' (szóköz) ír le.
A program írja ki a standard kimenetre a bejárható rész alapterületét, a falak hosszát és ajtók számát.
Beküldendő egy tömörített i235.zip állományban a program forráskódja (i235.pas, i235.cpp, ...), valamint a program dokumentációja (i235.txt, i235.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
(10 pont)
I. 236. Egy légitársaság adott napi járatainak útvonalát és utasainak számát vizsgáljuk. Az adatok rendelkezésünkre állnak az utvonal.txt, a kapcsolo.txt és a jarat.txt állományokban, melyek honlapunkról letölhetőek. Az állományok tabulátorral tagolt, UTF-8 kódolású szövegfájlok, az első sorok a mezőneveket tartalmazzák. (Az adatokat tartalmazó utvonal.txt, kapcsolo.txt és jarat.txt állományok.)
[1.] Készítsünk új adatbázist legitarsasag néven. Az előbb említett adatállományokat importáljuk az adatbázisba utvonal, kapcsolo és jarat néven.
[2.] Beolvasáskor állítsuk be a megfelelő adatformátumokat és kulcsokat. A táblákba ne vegyünk föl új mezőket.
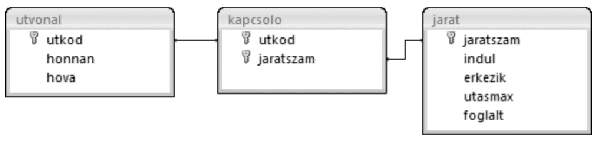
Táblák
utvonal (utkod, honnan, hova)
|
kapcsolo (utkod, jaratszam)
|
jarat (jaratszam, indul, erkezik, utasmax, foglalt)
|
Készítsük el a következő feladatok megoldását. Az egyes lekérdezéseknél ügyeljünk arra, hogy mindig csak a kért értékek jelenjenek meg, más adatok viszont ne. A megoldásokat a zárójelben lévő néven mentsük el.
[3.] Soroljuk fel ábécérendben, lekérdezés segítségével, hogy a légitársaság Budapestről mely városokba indít járatokat. A városok neve csak egyszer jelenjen meg a listában. (3celallomasok)
[4.] Melyik legkorábbi járaton van még szabad hely a Bécsből Londonba indulók közül? Adjuk meg a járatszámot, az indulási időt és a szabad helyek számát. (4koran)
[5.] Határozzuk meg, hogy az egyes városokban hány induló járatra lehet még jegyet kapni. (5varosonkent)
[6.] Melyik városba utaztatja a legtöbb utast a légitársaság? (6nepszeru)
[7.] Listázzuk ki azoknak a városoknak a nevét, amelyekbe Bécsből közvetlenül el lehet utazni, de Budapestről nem. (7atszallas)
[8.] Egy napon belül szeretnénk a Budapest ,-- ,Amszterdam ,-- ,Budapest utat megtenni. Soroljuk fel, hogy Amszterdamból milyen indulási idejű gépekre vehetünk jegyet, ha Budapestről a legkorábbi gépre van jegyünk és 2 óra elegendő az ottani ügyintézéshez. (8retur)
[9.] A Dubrovnikba érkező repülőgépek, a kedvező időjárás miatt, negyedórával előbb szállnak le. Készítsünk adatmódosító lekérdezést, amely az összes ilyen járat érkezési idejét ennek megfelelően módosítja. (9dubrovnik)
Beküldendő egy tömörített i236.zip állományban az adatbázis (i236.odb, i236.mdb), valamint egy rövid dokumentáció (i236.txt, i236.pdf), amelyből kiderül az alkalmazott adatbázis-kezelő neve, verziószáma.
(10 pont)
I. 237. A Magyar Tudományos Akadémia 185 éve alakult. A tudományos társaság eddigi tagjainak névsora és néhány adata a Wikipédia enciklopédiában elérhető. A 2948 akadémikus névsora nagyon hosszú, ezért 4 részletben érhető el a honlapon.
Készítsünk adattáblát az Akadémia élő tagjairól a Wikipédián közölt adatok összemásolásával, majd megfelelő, több lépéses konvertálásával. Az átalakításhoz a szövegszerkesztő és táblázatkezelő programok funkcióit és függvényeit használjuk, csak elkerülhetetlen esetben a kézi módosítást.
A tagsághoz, illetve annak kezdetéhez a felsorolásokból a legutolsó értékeket adjuk meg.
Minta:

Beküldendő egy tömörített i237.zip állományban egy táblázatkezelő munkafüzet (i237.xls, i237.ods, ...), illetve egy dokumentáció (i237.txt, i237.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziója, valamint az adatkonverzió lépéseinek leírása.
A helyes adattábla létrehozásáért 5 pont és a konverzió lépéseinek megadásáért szintén 5 pont kapható.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2010. április 12-én LEJÁRT. |
S. 52. Az ábra egy tavat ábrázol, amelyben egy kígyó rejtőzik. Az állat teste vízszintesen és függőlegesen tekereg, de saját magát még sarkosan sem érinti. A fekete mezők sziklák, melyeken a kígyó nem haladhat át. A táblázat alatti sorban lévő számok azt jelölik, hogy az adott oszlopban hány mezőben van kígyórész. A kígyó feje és farka adott, kilátszik a vízből.
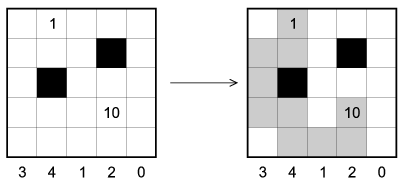
Készítsünk programot, amely megadja, hogy a kígyó hogyan helyezkedik el a vízben. A program a parancssor első argumentumaként megadott bemeneti állománya a tó és a kígyó ismert adatait tartalmazza. Az első sor a négyzet alakú tó N (3 N
N 20) oldalhosszát, a kígyó M (3
20) oldalhosszát, a kígyó M (3 M) méretét, míg a második sor négy, szóközzel ellátott E1, E2, V1 és V2 egész száma (1
M) méretét, míg a második sor négy, szóközzel ellátott E1, E2, V1 és V2 egész száma (1 E1,E2,V1,V2
E1,E2,V1,V2 N) a kígyó fejének és farkának koordinátáját adja meg. A harmadik sor K (0
N) a kígyó fejének és farkának koordinátáját adja meg. A harmadik sor K (0 K
K N) a vízben lévő sziklák számát, majd az ezt követő K darab sor mindegyike két egész számot, a sziklák koordinátáját tartalmazza. Az utolsó sor N darab számot tartalmaz, amelyek az oszlopok kígyórészeinek számát adja meg.
N) a vízben lévő sziklák számát, majd az ezt követő K darab sor mindegyike két egész számot, a sziklák koordinátáját tartalmazza. Az utolsó sor N darab számot tartalmaz, amelyek az oszlopok kígyórészeinek számát adja meg.
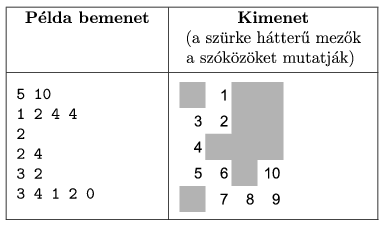
A parancssor második argumentumaként megadott kimeneti állomány N sorban a tavat, illetve a kígyó helyzetét jelenítse meg. A tó minden cellájának tartalmát három karakternyi helyre írjuk ki. A vizet szóközök, a kígyó testét a fejtől mért távolság ábrázolja.
Ha a feladatnak nincs megoldása, akkor a kimenet tartalma ,,Nincs megoldás'' legyen.
Beküldendő egy tömörített s52.zip állományban a program forráskódja (s52.pas, s52.cpp, ...), valamint a program dokumentációja (s52.txt, s52.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható.
Tesztállományok: kigyoteszt.zip
A feladat ötletének alapja a Magyar logikai rejtvények weboldalról származik.
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

