A KöMaL 2010. áprilisi matematika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
C-jelű feladatokA beküldési határidő 2010. május 10-én LEJÁRT. |
C. 1030. Az x, y valós számokra igaz, hogy x+3y=12 és x 2y
2y 0. Milyen értékeket vehet fel x+2y?
0. Milyen értékeket vehet fel x+2y?
(5 pont)
C. 1031. Egy fogadó az ötös lottón két szelvényen összesen tíz különböző számot jelölt meg. Ezek közül négyet ki is húztak. Mekkora annak a valószínűsége, hogy a fogadónak
a) négyes találata lett?
b) kettes találata lett?
(5 pont)
C. 1032. Egy háromszög B és C csúcsát kössük össze a szemközti oldalak harmadolópontjaival. Ezen szakaszok egy négyszöget határoznak meg. Bizonyítsuk be, hogy a négyszög egyik átlója párhuzamos a BC oldallal.
(5 pont)
C. 1033. Oldjuk meg az alábbi egyenletet: \(\displaystyle \log_{2010}\,(2009\,x)=\log_{2009}\,(2010\,x)\).
Javasolta: Pataki János (Budapest)
(5 pont)
C. 1034. Forgassunk meg egy szabályos hatszöget a szimmetriatengelyei körül. Hogyan aránylanak egymáshoz a keletkező forgástestek felszínei?
(5 pont)
 |
B-jelű feladatokA beküldési határidő 2010. május 10-én LEJÁRT. |
B. 4262. Adottak a P és Q pontok. Határozzuk meg a P-n átmenő összes e egyenes és a Q-ra illeszkedő, e-re merőleges Se sík metszéspontjának mértani helyét.
(3 pont)
B. 4263. Oldjuk meg az alábbi egyenletrendszert:
x3+4y=y3+16x,
(4 pont)
B. 4264. Az ABC háromszög C csúcsánál lévő szöge 120o. A háromszög magasságpontja M, a körülírt körének középpontja O, a kör ACB ívének felezőpontja pedig F. Bizonyítsuk be, hogy MF=FO.
(3 pont)
B. 4265. Színezzük ki a pozitív egész számokat 7 színnel úgy, hogy minden a pozitív egész számra az {a,2a,3a,4a,5a,6a,7a} halmaz elemeinek színe páronként különböző legyen.
(4 pont)
B. 4266. Jelölje a1, a2, a3, a4 a Pascal-háromszög egyik sorának négy, egymás után következő elemét. Igazoljuk, hogy az
számok számtani sorozatot alkotnak.
(3 pont)
B. 4267. Mutassuk meg, hogy egy háromszög oldalaira a hozzáírt körök érintési pontjaiban állított merőlegesek egy ponton mennek át.
Javasolta: Holló Gábor (Budapest)
(4 pont)
B. 4268. Határozzuk meg tizedestört alakjában a tizedesvessző utáni hatodik számjegyet.
(4 pont)
B. 4269. Szerkesszük meg az ABC háromszög AB oldalán azt a P pontot, amelyre a BCP és ACP háromszögekbe írható körök sugara egyenlő.
(5 pont)
B. 4270. Legyen ABCDEF egy körbe írt hatszög. Bizonyítsuk be, hogy
AD.BE.CF=AB.DE.CF+BC.EF.AD+CD.FA.BE+
+AB.CD.EF+BC.DE.FA.
(5 pont)
B. 4271. Van-e olyan legalább másodfokú polinom, amely a racionális számok halmazát kölcsönösen egyértelműen képezi le önmagára?
(5 pont)
 |
A-jelű feladatokA beküldési határidő 2010. május 10-én LEJÁRT. |
A. 506. Igazoljuk, hogy tetszőleges p prímszámra a pozitív egészeket ki lehet színezni p-1 színnel úgy, hogy minden a pozitív egész számra az
{a,2a,3a,...,(p-1)a}
halmaz elemeinek színe páronként különböző legyen.
(5 pont)
A. 507. A \(\displaystyle K_1,\dots,K_6\) körök ebben a sorrendben, kívülről érintik a \(\displaystyle K_0\) kört. Minden \(\displaystyle 1\le i\le 5\)-re a \(\displaystyle K_i\) és \(\displaystyle K_{i+1}\) körök kívülről érintik egymást, továbbá \(\displaystyle K_1\) és \(\displaystyle K_6\) is kívülről érintik egymást az ábra szerint. Jelöljük a \(\displaystyle K_i\) kör sugarát \(\displaystyle r_i\)-vel (\(\displaystyle 0\le i\le6\)). Igazoljuk, hogy ha \(\displaystyle r_1r_4=r_2r_5=r_3r_6=1\), akkor \(\displaystyle {r_0\le 1}\).
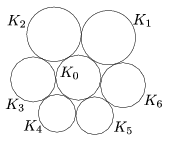
Javasolta: Strenner Balázs (Székesfehérvár)
(5 pont)
A. 508. A \(\displaystyle G\) gráfnak egy \(\displaystyle S\) feszített részgráfját ,,dominánsnak'' nevezzük, ha \(\displaystyle G\) minden \(\displaystyle S\)-en kívüli csúcsának van szomszédja \(\displaystyle S\)-ben. Létezik-e olyan gráf, aminek páros számú számú domináns részgráfja van?
Javasolta: Lovász László Miklós (Budapest)
(5 pont)
A matematika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

