A KöMaL 2010. májusi fizika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
M-jelű feladatokA beküldési határidő 2010. június 10-én LEJÁRT. |
M. 306. Méréssel határozzuk meg az egy egyenesbe eső két rúdmágnes között ható erő távolságfüggését!
Közli: Bakonyi Gábor, Budapest
(6 pont)
 |
P-jelű feladatokA beküldési határidő 2010. június 10-én LEJÁRT. |
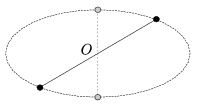
P. 4254. Amatőr csillagászok egy csoportja újonnan felfedezett kettőscsillagot vizsgál. Megfigyeléseik szerint a két csillag egy olyan fényes pontpárnak látszik, amely az ábra szerint egy ellipszispályát ír le az égen. Eszter, a csoport leglelkesebb tagja, nemrég tanult Kepler törvényeiről a középiskolában. Emlékei szerint az égitestek valóban ellipszis alakú pályákon mozognak, a vonzócentrumnak azonban nem az ellipszis \(\displaystyle O\) középpontjában, hanem az egyik fókuszpontban lenne a helye. Arra gyanakszik, hogy a két csillag valójában egy náluk sokkal nagyobb tömegű, az ellipszis gyújtópontjában elhelyezkedő, láthatatlan fekete lyuk körül kering. Igaza lehet-e Eszternek? Mi hogyan magyaráznánk a megfigyelést?
Közli: Vigh Máté, Pécs
(3 pont)
P. 4255. Milyen irányú és mekkora nagyságú az a legkisebb erő, amivel a vízszintes asztalon nyugvó, \(\displaystyle m\) tömegű kicsiny testet elhúzhatjuk az asztalon? A tapadási és a csúszási súrlódási tényező egyenlő, értéke\(\displaystyle ~\mu\).
Közli: Iván Dávid, Budapest
(4 pont)
P. 4256. Két fal között egy gumiszálat feszítünk ki. A szál \(\displaystyle C\) pontjában \(\displaystyle F\) nagyságú, szálirányú erőt fejtünk még ki.
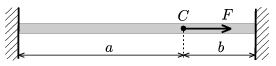
\(\displaystyle a)\) Mekkora a \(\displaystyle C\) pont elmozdulása, ha a szál \(\displaystyle D\) rugóállandóval jellemezhető?
\(\displaystyle b)\) A szál melyik pontjában hasson az \(\displaystyle F\) erő, hogy e pont elmozdulása a lehető legnagyobb legyen?
Adatok: \(\displaystyle F=5\) N, \(\displaystyle a=40\) cm, \(\displaystyle b=10\) cm, \(\displaystyle D=1~\frac{\rm N}{\rm cm}\).
Közli: Pálfalvi László, Pécs
(4 pont)
P. 4257. Üres félgömb belsejében egy keskeny karika csúszásmentesen gördül le, valamelyik vízszintes átmérőjének egyik végpontjából. Mekkora sebességgel ér le a gömb mélypontjába? A karika sugara \(\displaystyle r=2\) cm, a félgömb sugara \(\displaystyle n=4\)-szer nagyobb, mint a karikáé. A félgömb rögzített, átmérősíkja vízszintes.
Strasser V. Benő (1884-1966) feladata
(4 pont)
P. 4258. Három, páronként egymásra merőleges rúd a vízszintes, érdes talajon gúlába rakva áll, és a gúla csúcsa \(\displaystyle Q\) súlyt tart. Mekkora erő hat az egyes rudakban, ha azok egyenlő hosszúak, illetve ha különböző hosszúságúak? (A rudak súlya \(\displaystyle Q\)-hoz képest elhanyagolható.)
Nagy Béla (1881-1954) feladata
(5 pont)
P. 4259. Miért lehetséges - kellő lendülettel való - felugrás után a levegőben ,,bukfencet vetni'' (szaltózni), és azután talpra esni?
Faragó Andor (1877-1944) feladata
(4 pont)
P. 4260. Súrlódás nélkül mozoghat a vízszintes \(\displaystyle X\) tengely mentén egy \(\displaystyle m\) tömegű test. \(\displaystyle L\) hosszúságú fonállal kapcsolódik hozzá egy másik \(\displaystyle m\) tömegű test, amely a függőleges \(\displaystyle Y\) tengely mentén tud csak elmozdulni. Kezdetben ez a test az origóban áll, a másik pedig tőle \(\displaystyle L\) távolságra, az \(\displaystyle X\) tengelyen. Ezután a testeket magukra hagyjuk.
Mekkora sebességre gyorsul fel az egyik és mekkorára a másik test a nehézségi erő hatására? Milyen mozgást végeznek a testek?
Közli: Radnai Gyula, Budapest
(5 pont)
P. 4261. Egyik végén zárt, 15 cm sugarú fémhenger 50 cm hosszú. Egy könnyen mozgó dugattyú a henger zárt végétől 40 cm-re normál állapotú levegőt zár el a külvilágtól. A bezárt levegőt egy 100 W-os fűtő 80%-os hatásfokkal melegíti. Mennyi idő alatt tolja ki a levegő a hengerből a dugattyút?
Közli: Szombathy Miklós, Eger
(4 pont)
P. 4262. Síkkondenzátor vízszintes lemezei közé a lemezek felezősíkjában egy elektront lövünk be \(\displaystyle v_{0}=4\cdot 10^7\) m/s kezdősebességgel. Az ismeretlen lemeztávolságú és lemezhosszúságú kondenzátorra \(\displaystyle U=500\) V egyenfeszültséget kapcsoltunk. Ha a lemezek közötti térben megfelelő irányítású, \(\displaystyle B=6{,}25\cdot 10^{-5}\) Vs/m\(\displaystyle {}^2\) indukciójú homogén mágneses mezőt hozunk létre, a belőtt elektron irányváltoztatás nélkül, állandó sebességgel halad át a síkkondenzátoron.
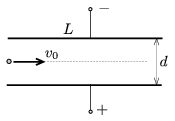
\(\displaystyle a)\) Határozzuk meg a síkkondenzátor lemezei között az elektromos térerősség nagyságát!
\(\displaystyle b)\) Mekkora a kondenzátor lemezei közti \(\displaystyle d\) távolság?
\(\displaystyle c)\) A mágneses mező kiiktatása esetén a kondenzátor lemezei között az elektron sebessége 0,6%-kal megnő. Határozzuk meg a síkkondenzátor lemezeinek \(\displaystyle L\) hosszát!
Közli: Kotek László, Pécs
(4 pont)
P. 4263. 2000 menetes, 0,5 m középkör sugarú, \(\displaystyle 2~cm^2\) keresztmetszetű toroid (körtekercs) áramának egyenletes változási sebessége 10 A/s. Mekkora gyorsulással indul el a körtekercs középpontjában nyugvó proton, illetve elektron?
Útmutatás: A toroid változó mágneses tere által keltett elektromos tér hasonló szerkezetű, mint a köráram mágneses tere.
Közli: Holics László, Budapest
(5 pont)
A fizika gyakorlatok és feladatok megoldásait honlapunkon keresztül küldheted be:
- megszerkesztheted vagy feltöltheted az Elektronikus munkafüzetben.
(Az interneten keresztül történő beküldésről olvasd el tájékoztatónkat)

