A KöMaL 2010. szeptemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2010. október 11-én LEJÁRT. |
I. 244. Geometrikus elemekből álló és kevés színt tartalmazó ábrákat tömörítve tárolunk. Minden egyes sorról csak azt tartalmazza a tömörített állomány, hogy mi változott az előző sorhoz képest. Ha egy sor megegyezik az előzővel, akkor a tömörített állományban erről nem szerepel bejegyzés.
A honlapunkról letölthető zaszlo5.be állomány első sorában a kép sorainak száma, N (1 N
N 100) és oszlopainak száma, M (1
100) és oszlopainak száma, M (1 M
M 100) van. A következő sorok a kódolt képet tartalmazzák, soronként és azon belül oszloponként növekvő sorrendben. Az első szám a tömörítetlen kép megfelelő sorát jelenti, a második és a harmadik szám kezdő és végpozíciót, amelyen belül a negyedik nagybetű szerepel.
100) van. A következő sorok a kódolt képet tartalmazzák, soronként és azon belül oszloponként növekvő sorrendben. Az első szám a tömörítetlen kép megfelelő sorát jelenti, a második és a harmadik szám kezdő és végpozíciót, amelyen belül a negyedik nagybetű szerepel.
Például:

Készítsünk programot i244 néven, amely az alábbi problémákat oldja meg, a parancssor első argumentumaként megadott zaszloX.be állományban talált adatok felhasználásával.
Minden részfeladat megoldása előtt írja a képernyőre a feladat sorszámát (például 3. feladat: ).
1.] Olvassuk be és megfelelő adatszerkezetben tároljuk el a bemeneti adatállomány tartalmát.
[2.] Állítsuk elő és írjuk ki a képernyőre a tömörítetlen ábrát. A betűk között egy-egy szóköz legyen.
[3.] Írjuk ki, hogy melyik színből (betűből) hány darab van az ábrán.
[4.] A parancssor második argumentumaként megadott kimeneti zaszloX.ki állományba másik tömörítési módszerrel mentsük el az ábra kódját. Az N soros ábra tömörített állománya N sorból álljon. Minden sorban szóközzel elválasztva egy-egy színt megadó nagybetű és az egymás utáni ismétlődések száma következik.
Például a fenti dán zászló tömörítve:

[5.] A program kérje be az ábra egy pontjának koordinátáját és írja ki annak a színét és azt, hogy mekkora azonos színű összefüggő területhez tartozik. A színezés csak oldalszomszédos egyezőség esetén összefüggő.
[6.] Jelenítsük meg a képernyőn kétszeres méretben az ábrát, azaz az eredeti ábra minden pontjának, betűjének vízszintesen és függőlegesen is két-két betű feleljen meg.
Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét röviden bemutató dokumentáció (i244.txt, i244.pdf, ...) egy tömörített mappában (i244.zip).
(A 2009. évi programozás OKTV 2. fordulójának feladat ötlete alapján)
(10 pont)
I. 245. A Pletyka utca új, hatlakásos társasházába nemrég költöztek be a lakók. Mindegyikük szívesen átjár a másikhoz egy kis beszélgetésre. A vendég mindent elmond magáról és az általa már ismert lakótársakról, többek között azt is, hogy melyik család honnan költözött oda. Természetesen a házigazda is megosztja a vendéggel saját hasonló ismereteit.
Határozzuk meg, melyik találkozást követően fogja mindenki mindenkiről tudni, hogy honnan költözött a házba.
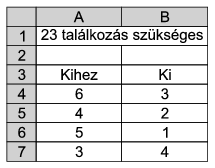
A megoldást táblázatkezelő program segítségével adjuk meg. A táblázat 3. sorától soronként egy-egy találkozást jegyzünk be. Az A oszlopba annak a lakásnak a sorszámát írjuk, amelybe ellátogatott a B oszlopban szereplő lakásból valaki. (A lakások sorszáma 1, 2, ..., 6).
Az eredményt az A1-es cellában jelenítsük meg a mintán látható formában. Ha a bejegyzett találkozások nem elegendők a ,,kívánt'' állapot kialakulásához, a cella maradjon üresen.
A megoldás során segédcellák használata megengedett, saját függvény és makró nem használható. Feltételezhetjük, hogy legfeljebb 300 találkozást jegyzünk be a táblázatba.
Beküldendő a táblázatkezelő munkafüzet (i245.xls, i245.ods, ...), illetve egy rövid dokumentáció (i245.txt, i245.pdf, ...), amelyben szerepel a megoldáskor alkalmazott táblázatkezelő neve, verziószáma, valamint a megoldás rövid leírása egy tömörített (i245.zip) állományban.
(10 pont)
I. 246. A következő játékot egy személy játssza egy N×N méretű táblázatban. Kezdetben a táblázat minden cellája kék színű. Ha egy cellára rákattintunk, ennek a cellának és oldalszomszédainak színe megváltozik. Ha egy cella kék volt, akkor piros lesz, ha piros, akkor pedig kék. A cél egy adott állapot elérése.
Készítsük el a játék weblapon játszható változatát. Az oldalon -- a betöltését követően -- jelenítsünk meg két táblázatot. Az egyik táblázat -- amelynek állapotát a játékos módosíthatja -- minden cellája legyen kék. A másik táblázat mutassa a célállapotot. A célállapotot véletlenszerűen alakítsuk ki, biztosítva a megoldhatóságot. A játékos az első táblázat celláira kattintva megpróbálja elérni a célállapotot. Ha sikerrel járt, akkor írjuk ki, hogy hány lépésben adta meg a megoldást és jelezze, ha kevesebb lépésben is el lehetett volna érni azt.
A feladat megoldásánál a html és a javascript elemei használhatók.
Beküldendő az i246.html dokumentum és az esetlegesen szükséges GIF, JPEG vagy PNG formátumú képfájlok, valamint a megoldás rövid dokumentációja (i246.txt vagy i246.pdf) egy i246.zip fájlba tömörítve.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2010. október 11-én LEJÁRT. |
S. 55. Közismert, hogy egy huszárral be tudjuk járni a sakktábla összes mezőjét úgy, hogy minden mezőt pontosan egyszer érintünk. Erre könnyen megjegyezhető, egyszerű algoritmus áll rendelkezésre. A megoldandó feladat most ennél bonyolultabb. Az első néhány lépést már megtették helyettünk.
Írjunk programot, amely megkeresi a megkezdett út leghosszabb folytatását. A program első parancssori paramétere az eddigi utat tartalmazó fájl neve, a második parancssori paraméter pedig az út folytatását tartalmazó fájl neve. Mindkét fájl ugyanolyan szerkezetű, az első sor tartalmazza a tárolt lépések (L) számát, a második sorban pedig az érintett L darab mező következik egymástól egy-egy szóközzel elválasztva, a lépések sorrendjében.
|
[] A sakktábla mérete 6×6, a mezők jelölése a játékban megszokottnak megfelelő.
[] A bemeneti fájl utolsó felsorolt mezője és a kimeneti fájl első mezője egyezik.
[] Ha az út nem folytatható, akkor az első sorba az 1 kerüljön, a másodikba pedig az a mező, ahol a huszár éppen áll.
Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét röviden bemutató dokumentáció (s55.txt, s55.pdf, ...) egy tömörített mappában (s55.zip).
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

