KöMaL Problems in Informatics, October 2010
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'I'Deadline expired on November 10, 2010. |
I. 247. Two successive photocells and a camera for reading off number plates are installed both at the entrance and at the exit of an automated paid parking lot. Any vehicle passing through a gate activates both photocells so that both crossing time instants and the number plate are recorded in a text file.
One has to pay for parking between 8:00:00 and 17:59:59. The remaining period is for free, nevertheless recording takes place all day for security reasons.
The file contains data recorded on a specific day. Each line of the file contains the time instants (in an hour-minute-second format) of crossing the outer and inner photocells together with the registration identifier from the number plate.
The meaning of the first line of the example is the following: a vehicle crossed the outer photocell at 3:32:42, and the inner one at 3:32:44. Since the latter occurred later, the vehicle entered the parking lot. The second line of the example tells us that vehicle JOJ-962 left the parking area.
3 32 42 3 32 44 JLQ-960
3 45 16 3 45 13 JOJ-962
3 57 3 3 57 1 AJA-221
...
Your program i247 should solve the following tasks. When writing on the screen, the number of the actual task (e.g. ,,Task #3'') should always be displayed.
1. Read the data from file parkolo.be, then solve the tasks below.
2. For each line of the text file, determine whether the actual vehicle entered of left the parking place. Display the registration identifiers together with either ,,In'' or ,,Out''.
3. Display the hour in which the most vehicles entered the parking lot.
4. Determine the number of different registration identifiers passing through the gates.
5. Summarize parking times during the day for vehicles leaving the parking place at least once. Display this information together with the registration identifier of the vehicle spending the most time inside.
6. Determine for each exit whether the vehicle has to pay and for how many hours. (At the beginning of each new hour the next 60 minutes will have to be completely paid.) Results should be written into the text file parkolo.ki as pairs of registration identifiers and the corresponding number of hours.
The source code (i247.pas, i247.cpp, ...) together with a short documentation (i247.txt, i247.pdf, ...) -- also describing which developer environment to use for compiling, further a brief description of your solution--should be submitted in a compressed file (i247.zip).
(10 pont)
solution (in Hungarian), statistics
I. 248. There is a single continuous black curve on an N×N black and white image (the number of pixels, N is  100). We know only the chain code of the curve and we have to recover the original image.
100). We know only the chain code of the curve and we have to recover the original image.
The chain code of a curve is briefly described in the following. The code contains the coordinates of the starting point and the successive directions obtained as we travel along the curve. The starting point is any of the endpoints of the curve. As we travel along the curve from the starting point to the other endpoint, we note the direction in each step. The figure shows the 8 possible directions.
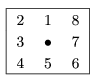
By using a spreadsheet application, you should recover the image if the chain code of the curve is known.
The sheet ,,In'' should contain the following pieces of information:
-- coordinates of the starting point
-- successive directions, so that they can be entered below each other
-- auxiliary sheets and computations needed to produce the image. You should take into account the maximal possible size of the image.
Then you should prepare a sheet ,,Out'' to display the image. You should adjust column width and row height such that cells are displayed as squares. All cells should be visible on the screen. Cells that are part of the curve can be denoted by an arbitrary character. The example shows a possible input (,,Be munkalap'') and output (,,Ki munkalap'').
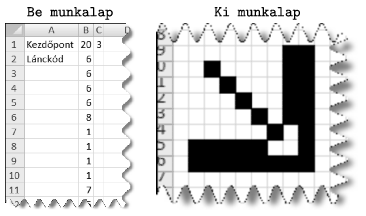
Your solution may not contain macros or program modules, only formulae and built-in functions. All auxiliary computations should be visible and nothing should be hidden.
Your spreadsheet (i248.xls, i248.ods, ...) together with a short documentation (i248.txt, i248.pdf, ...) -- also describing the name and version number of the spreadsheet application, further a brief description of your solution -- should be submitted.
(10 pont)
solution (in Hungarian), statistics
I. 249. A regular expression is a pattern that can match a set of strings (see e.g. http://en.wikipedia.org/wiki/Regular_expression). They are suitable, for example, to check the structure of certain texts (e.g. email addresses, URLs).
The following tasks from a) to h) should be solved by giving a suitable regular expression. If there is more than one solution, your aim is to choose the regular expression consisting of the least number of characters, if possible.
You should use the following files (each line of them is correct):
-- kartya.txt: successive lines of the file contain the French playing cards in a format suit, space, rank.\ For example: hearts ace, diamond king, spades 10, clubs jack.
-- email.txt: lines of the file contain an email address. \ For example: headmaster@school.hu.
-- telefon.txt: lines of the file contain a telephone number. \ For example: (30)555-55-55, or (46)555-555.
-- rendszam.txt: lines of the file contain registration identifiers from number plates.\ For example: KUTYA-1, PAPA-05, ABC-123.
You should display all lines of the appropriate files that satisfy the following constraints:
a) the registration identifier contains ,,A'' and ,,3'';
b) contain a registration number of the form 3 letters, hyphen, 3 digits;
c) contain a red suit (hearts or diamond);
d) contain a playing card with a number;
e) contain a mobile phone number (possible district numbers are 20, 30 or 70);
f) do not contain a mobile phone number;
g) contain only the lowercase letters of the English alphabet, and possibly ,,@'' (at) and ,,.'' (full stop), further, they end in ,,.hu'';
h) email addresses of the form ,,firstname.lastname@...'' where the last name is ,,kovacs''.
The above tasks are not in order of increasing difficulty. Your solution will be checked by the program egrep, freely downloadable under Windows and Linux.
The following simple example shows how to use egrep:
egrep "[0-9]" kodok.txt
for example finds all lines of the file kodok.txt that contain at least one digit.
You should submit a file i249.txt, containing your solutions to the above tasks from a) to h), further, the name of the operating system and the actual version number of the program egrep used for testing.
(10 pont)
 |
Problems with sign 'S'Deadline expired on November 10, 2010. |
S. 56. You are given the road map of a town with junctions and the two-way streets connecting them. You would like to travel all junctions (but all streets do not have to be travelled) with a bus that can not go reverse, so it can not return to the junction immediately visited. (Otherwise all streets and junctions can be visited arbitrarily.)
Your program should read the road map of the town from the standard input, then determine a sequence of junctions that contain all of them, consecutive junctions are directly connected, but there is no ,,direct return'' (in the sense that there are no 3 consecutive junctions in the sequence with the first and third being the same). We can assume that any two junctions are connected by at most one street, the road map is connected (that is, one can travel from any junction to any other), further, there is no dead end in the town (that is, a junction connected to only one street).
The first line of the input contains 2 integers separated by a space, the number of junctions in the town and the number of streets
. Then each of the following M lines contains the two endpoints Xi, Yi of a street (separated by a space) with 1
 Xi
Xi Yi
Yi N.
N.
The only line of the standard output should be the sequence of junctions satisfying the above criteria.
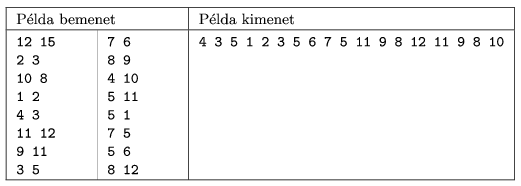
We have given a sample input (Példa bemenet) and a possible output (Példa kimenet).
The source code and project files of your solution -- without the .exe or any other auxiliary files generated by the compiler -- should be submitted together with a short documentation (s56.txt, s56.pdf, ...) in a compressed folder s56.zip.
(10 pont)
$Var(Body)
Upload your solutions above
