KöMaL Problems in Mathematics, October 2010
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'K'Deadline expired on November 10, 2010. |
K. 259. ABCD and EFGH are coplanar rectangles with parallel sides. Given that AB=15 cm, AD=12 cm, EF=10 cm, EH=8 cm, FI=14 cm, calculate the difference of the shaded areas.
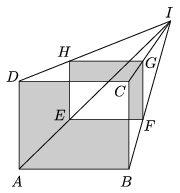
(6 pont)
solution (in Hungarian), statistics
K. 260. In a certain class, more than 93% of the students are girls but there are boys, too. What is the smallest possible number of students in the class if the number of girls is an integer percentage of it?
(6 pont)
solution (in Hungarian), statistics
K. 261. There are four numbers listed on a sheet of paper. The mean of the first two, the last two, and the middle two is 7, 8.4, and 2.3, respectively. What is the mean of the first and last numbers?
(6 pont)
solution (in Hungarian), statistics
K. 262. The entrance to the Happy Holidays Campsite lies right next to a straight road. The entrance to the Sweet Summer Youth Camp lies 300 metres off the road. The distance between the two entrances is 500 as the crow flies. A restaurant is to be built right next to the road. Where should it be built so that it is equidistant from the entrances of the campsite and the youth camp?
(6 pont)
solution (in Hungarian), statistics
K. 263. Charles writes the numbers 3, 5, 6 on three cards, and Charlotte writes the numbers 8, 9, 10 on three cards. Each of them selects two cards at random out of the three of their own. Charles multiplies his two numbers, and Charlotte adds hers. What is the probability that Charles will get a greater number than Charlotte?
(6 pont)
solution (in Hungarian), statistics
K. 264. In a canning factory, four cylindrical tin cans are fixed together with a plastic tape wound about them in the ways shown in the figures.
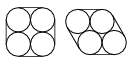
What length of plastic tape is needed in each case if the diameter of the base of the cylinders is 10 cm, and 2-cm lengths of tape overlap at the ends?
(6 pont)
 |
Problems with sign 'C'Deadline expired on November 10, 2010. |
C. 1045. Three regular dice are rolled. The three numbers obtained on top are listed in an arbitrary order. Then the list is continued with the numbers obtained on the bottom, in the same order. The resulting six-digit number is divided by 111, 7 is subtracted from the ratio, and the difference is divided by 9. Prove that the result is a three-digit number whose digits are the numbers rolled.
(5 pont)
solution (in Hungarian), statistics
C. 1046. Let  (n) denote the measure of the interior angles of a regular n-sided polygon. What is n if
(n) denote the measure of the interior angles of a regular n-sided polygon. What is n if  (n+3)-
(n+3)- (n)=
(n)= (n)-
(n)- (n-2)?
(n-2)?
(5 pont)
solution (in Hungarian), statistics
C. 1047. A fair coin is tossed ten times in a row. Every time a head is tossed, a digit of 2 is written down. When a tail is tossed, a digit of 3 is written down. What is the probability that the resulting ten-digit number is divisible by a) 3, b) 4?
(5 pont)
solution (in Hungarian), statistics
C. 1048. Prove that .
(5 pont)
solution (in Hungarian), statistics
C. 1049. Consider the circles drawn on two adjacent sides of a square of side 2 units. Find the radius of the circle that touches one of the sides and one circle from the inside and the other circle from the outside.
(5 pont)
 |
Problems with sign 'B'Deadline expired on November 10, 2010. |
B. 4292. The feet of the perpendiculars dropped from vertex C of triangle ABC onto the interior angle bisectors from vertices A and B are E and F, respectively. The inscribed circle of the triangle touches side AC at point D. Prove that EF=CD.
(3 pont)
solution (in Hungarian), statistics
B. 4293. The sum of three positive integers is 2010, and the sum of their reciprocals is . What are these numbers?
(Italian competition problem)
(5 pont)
solution (in Hungarian), statistics
B. 4294. What is the maximum number of edges of a regular decagonal right prism that a plane may intersect?
(3 pont)
solution (in Hungarian), statistics
B. 4295. A 13×13 table is filled in with numbers, such that the sum of the numbers is the same in each of the 13 rows and 13 columns. What is the smallest possible number of fields in which the entries should be changed so that the 26 sums are all different?
(Based on a problem of the "Kavics Kupa" Competition, 2010)
(5 pont)
solution (in Hungarian), statistics
B. 4296. Let ma and mb denote the lengths of the altitudes drawn to sides a and b of a triangle. Show that if a>b then a2010+ma2010 b2010+mb2010.
b2010+mb2010.
(4 pont)
solution (in Hungarian), statistics
B. 4297. Prove that for all real numbers x and y.
(4 pont)
solution (in Hungarian), statistics
B. 4298. Given a regular pentagon, find the point for which the sum of the distances from the vertices of the pentagon is minimal.
(Balázs Csikós, Budapest)
(4 pont)
solution (in Hungarian), statistics
B. 4299. Parallelogram CDEF is inscribed in triangle ABC, with vertices D, E, F lying on sides CA, AB and BC, respectively. Given the length of the line segment DF, construct the point E. For what point E will the length of diagonal DF be minimal?
(Sándor Katz, Bonyhád)
(5 pont)
solution (in Hungarian), statistics
B. 4300. Prove that the sum of the squares of 35 consecutive positive integers is always divisible by 35.
(3 pont)
solution (in Hungarian), statistics
B. 4301. The difference of the cubes of two consecutive positive integers is n2, where n>0. Prove that n is the sum of two perfect squares.
(Kalmár Competition 8th grade, regional round, 2010)
(4 pont)
 |
Problems with sign 'A'Deadline expired on November 10, 2010. |
A. 515. There is given a triangle ABC. For every 0<t<1 let U(t) and V(t) be the points which divide the line segments AB and BC in the ratio t:(1-t), respectively. Prove that there is a parabola which is tangent to all lines U(t)V(t).
(5 pont)
A. 516. In each of five boxes B1, B2, B3, B4, B5 there is initially one coin. There are two types of operation allowed:
Type 1: Choose a nonempty box Bj with 1 j
j 4. Remove one coin from Bj and add two coins to Bj+1.
4. Remove one coin from Bj and add two coins to Bj+1.
Type 2: Choose a nonempty box Bk with 1 k
k 3. Remove one coin from Bk and exchange the contents of (possibly empty) boxes Bk+1 and Bk+2.
3. Remove one coin from Bk and exchange the contents of (possibly empty) boxes Bk+1 and Bk+2.
Prove that for every integer 0 n
n 22010 there is a finite sequence of such operations that results in boxes B1, B2, B3, B4 being empty and box B5 containing exactly n coins.
22010 there is a finite sequence of such operations that results in boxes B1, B2, B3, B4 being empty and box B5 containing exactly n coins.
(5 pont)
solution (in Hungarian), statistics
A. 517. Let m 3 be a positive integer, and let
3 be a positive integer, and let 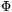 m(x) be the mth cyclotomic polynomial, and denote by
m(x) be the mth cyclotomic polynomial, and denote by 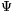 m(x) the polynomial with integer coefficients for which
m(x) the polynomial with integer coefficients for which . Prove that for every integer a, any prime divisor of the number
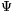 m(a) either divides m or is of the form mk
m(a) either divides m or is of the form mk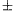 1.
1.
(5 pont)
Upload your solutions above.
