A KöMaL 2010. novemberi informatika feladatai
Kérjük, ha még nem tetted meg, olvasd el a versenykiírást.
Feladat típusok elrejtése/megmutatása:
 |
I-jelű feladatokA beküldési határidő 2010. december 10-én LEJÁRT. |
I. 250. Legyen egy N×M (5 N,M
N,M 100) téglalap alakú lemezünk, amelyben a repedések terjedését szeretnénk szimulálni.
100) téglalap alakú lemezünk, amelyben a repedések terjedését szeretnénk szimulálni.
A téglalapot töltsük fel közötti véletlen számokkal. A téglalap oldalainak maximális értékű pontjaiból fognak a repedések kiindulni. Ha több maximális értékű pont van egy oldalon, akkor egyszerre onnan több repedés indul ki. A repedések az oldaltól függő irányba növekszenek tovább. Például az alulról induló repedés csak balra fel, vagy fel, vagy jobbra fel terjedhet. A jobbról érkező repedés balra fel, balra, vagy balra le, a többi irányból hasonlóan elv szerint terjedhet.
Alulról érkező repedés választható lépése vastagon keretezve:
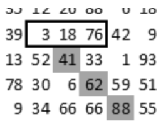
A három választható szám közül a maximális érték irányába folytatódik a repedés. Ha azonos számokat talál, akkor ezek irányában szétágazik. Ha eléri a téglalap szélét vagy már egy kialakult repedésbe fut bele, akkor ott a terjedés megáll.
Készítsünk programot, amely az N×M téglalapban a repedések kialakulását mutatja be.
A program első két argumentuma N és M értéke, a harmadik egy kimeneti fájl legyen. A kimeneti fájlban jelenítsük meg a véletlen számok mátrixát és a mintán látható módon a repedések képét. A megjelenítés során a repedést ,,X'' és többi pontot ,,.'' karakter ábrázolja. A számok, illetve a karakterek között egy-egy szóköz legyen.
Lehetséges eredmény 10×10-es lemez repedésekor:
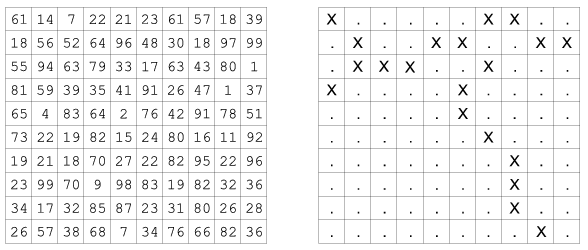
Beküldendő a program forráskódja (i250.pas, i250.cpp, ...), valamint a program rövid dokumentációja (i250.txt, i250.pdf, ...), amely tartalmazza a megoldás rövid leírását, és megadja, hogy a forrásállomány melyik fejlesztő környezetben fordítható egy tömörített i250.zip mappában.
(10 pont)
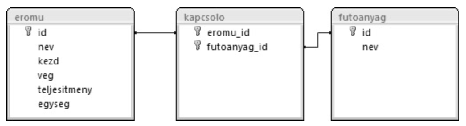
I. 251. A magyarországi villamos erőművek adatai állnak rendelkezésünkre az eromu.txt, a kapcsolo.txt és a futoanyag.txt állományokban. Az állományok tabulátorral tagolt, UTF-8 kódolású szövegfájlok, az első sorok a mezőneveket tartalmazzák.
[1.] Készítsünk új adatbázist i251 néven. A mellékelt adatállományokat importáljuk az adatbázisba a forrásállományokkal azonos néven.
[2.] Beolvasáskor állítsuk be a megfelelő adatformátumokat és kulcsokat. A táblákba ne vegyünk fel új mezőt.

Készítsük el a következő feladatok megoldásait. Az egyes lekérdezéseknél ügyeljünk arra, hogy mindig csak a kért értékek jelenjenek meg és más adatok viszont ne. A megoldásokat a zárójelben lévő néven mentsük el.
[3.] Soroljuk fel ábécérendben, lekérdezés segítségével, a megújuló energiaforrással, azaz biomasszával vagy vízzel üzemeltetett erőművek nevét. (3megujulo)
[4.] Melyik a legnagyobb teljesítményű erőművünk? Adjuk meg a nevét és a teljesítményét. (4legnagyobb)
[5.] Lekérdezéssel határozzuk meg, hogy melyek azok az erőművek, amelyek ugyanolyan fűtőanyagot használnak, mint a ,,Mátrai Erőmű''. (5matrai)
[6.] Adjuk meg fűtőanyagonként, hogy ha csak az az energiaforrás állna rendelkezésre, mennyi lenne az erőművek együttes teljesítménye. A fűtőanyag és összes teljesítmény lista az utóbbi szerint csökkenően jelenjen meg. (6tipusonkent)
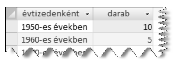
[7.] Készítsünk lekérdezést, amely megadja, hogy évtizedenként hány erőművet helyeztek üzembe? (7szakaszok)
Példa: Az 1960-as évek az 1960-tól 1969-ig tartó éveket jelenti.
[8.] A barnaszénnel működő erőművek a környezetet erősen terhelik, ugyanakkor alacsony fűtőértékűek, ezért a felhasználását megszüntetik. Az adatbázis karbantartásához, egymás utáni végrehajtást feltételezve, három törlő lekérdezést készítsünk. A törlő lekérdezéseket lefuttatni nem szükséges, de megengedett.
[\(\displaystyle a.\)] Töröljük, lekérdezés segítségével a kapcsolo táblából azokat a rekordokat, ahol a barnaszén felhasználásához volt kapcsolat. ("8barna_1")
[\(\displaystyle b.\)] Töröljük a futoanyag táblából a barnaszén rekordját. ("8barna_2")
[\(\displaystyle c.\)] Töröljük az eromu táblából azoknak az erőműveknek az összes adatát, amelyeket be kell zárni, mert nem maradt más fűtőanyag típusuk. ("8barna_3")
Beküldendő az adatbázis (i251.odb, i251.mdb, ...), valamint egy rövid dokumentáció (i251.txt, i251.pdf, ...), amelyből kiderül az alkalmazott adatbázis-kezelő neve, verziószáma egy tömörített i251.zip mappában.
(10 pont)
I. 252. Egy a Manhattant építő munkások pihenőjét megörökítő híres kép letölthető pl. a következő helyről: http://jeanettteigen.files.wordpress.com/ 2010/10/eating-above-manhattan-post2.jpg. A képet alakítsuk át úgy, hogy az eredeti munkások helyett az osztályunk vagy baráti körünk tagjai szerepeljenek rajta. Az eredeti munkások mindegyikét retusáljuk le a képről, tehát vagy a háttér egyes részeit, vagy a mi társaságunkból származó személyt lehessen látni. Természetesen csalhatunk, azaz megjelenhetnek épület-- és háttérrészletek ott is, ahol az eredeti képen nem voltak, pl. azért, hogy egy kilógó lábat eltakarjunk. A végső kép az eredetihez hasonló fekete-fehér fényképhez legyen hasonló, 800×600-as méretben. A feladat megoldásához a Gimp képszerkesztőt használjuk, amely szabadon használható és letölthető a http://www.gimp.org oldalról.
Beküldendő a retusálás eredményeként létrejövő Gimp formátumú (i252.xcf) állomány, valamint az ott megjelenő társaságról készült eredeti JPEG kép (i252tars.jpg), mindkettő 800×600-as méretben, egy tömörített i252.zip mappában. A feladat megoldásakor ügyeljünk arra, hogy a beküldendő tömörített állomány mérete legföljebb 2MB lehet.
(10 pont)
 |
S-jelű feladatokA beküldési határidő 2010. december 10-én LEJÁRT. |
S. 57. Egy sakktáblát szeretnénk lefedni (hézagmentesen és átfedések nélkül) dominókkal úgy, hogy a tábla bizonyos mezőit kizártuk (a kizárt mezőkre nem kerülhet dominó).
Készítsünk programot, amely a standard bemenetről beolvassa a tábla méretét, valamint a kizárt mezőket, és kiszámít egy megfelelő lefedést, amennyiben létezik.
A bemenet szerkezete a következő: Az első sorban két, szóközzel elválasztott egész szám, a tábla mérete (1 N
N 100), és a kizárt mezők (0
100), és a kizárt mezők (0 M
M N.N) száma található. A következő M sor mindegyikében, szóközzel elválasztva, egy-egy kizárt mező sor és oszlop koordinátái szerepelnek (1
N.N) száma található. A következő M sor mindegyikében, szóközzel elválasztva, egy-egy kizárt mező sor és oszlop koordinátái szerepelnek (1 I,J
I,J N).
N).
Ha létezik megfelelő lefedés, akkor a standard kimenetre írjunk ki N sort, amelyek mindegyikében N szám található. Az i. sor j. száma a sakktábla i. sorának j. mezőjét lefedő dominó sorszáma, ha az adott mező nem kizárt, egyébként 0. A dominók sorszámozása tetszőleges (különböző dominók különböző sorszámot kell, hogy kapjanak). Ha nem létezik megfelelő lefedés, akkor a ,,nem fedhető le'' szöveget írjuk ki. A futási időlimit tesztesetenként 10 másodperc.
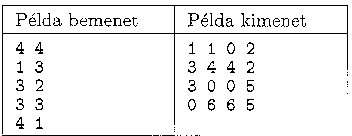
Beküldendő a feladat megoldását tartalmazó forrás és projektállományok (az .exe és más a fordító által generált kiegészítő állományok nélkül), valamint a megoldás menetét röviden bemutató dokumentáció egy s57.zip tömörített mappában.
Értékelés: 8 pont szerezhető az olyan programmal, ami bármilyen (a fenti feltételeknek megfelelő) tesztesetet képes megoldani (ha a futásidő túllépi a 10 mp-t, akkor úgy tekintjük, hogy nem tudta megoldani az adott tesztesetet). A legföljebb 10×10-es táblákat megoldó program 5 pontot ér. További 2 pont szerezhető a dokumentációval.
Tesztesetek és kimeneteik a feladathoz: s57teszt.zip
(10 pont)
Figyelem!
Az informatika feladatok megoldásait ne e-mailben küldd be! A megoldásokat az Elektronikus munkafüzetben töltheted fel.

