KöMaL Problems in Physics, December 2010
Please read the rules of the competition.
Show/hide problems of signs:
 |
Problems with sign 'M'Deadline expired on January 10, 2011. |
M. 310. Put a ping-pong ball onto the surface of the water in a glass, filled halfway. We experience that the ball moves next to the wall of the glass. Then fill the glass up to its rim, and place the ball again to the water. We can see that the ball moves to the centre of the glass. Examine experimentally, whether we experience the same or not if instead of the glass we use a wider vessel, for example a pot? What is the width of that vessel in which the experiment still ``works''? How does the time during which the ball moves to the wall, depends on the initial distance between the ball and the wall?
(6 pont)
 |
Problems with sign 'P'Deadline expired on January 10, 2011. |
P. 4295. When a ruler is supported from below, 15 cm from one of its ends, then the ruler can be balanced with two alike coins, placed 5 cm from the end of the ruler. When the support is placed 1 cm from the same end of the ruler it can be balanced with six alike coins, at the same position. How long is the ruler?
(3 pont)
solution (in Hungarian), statistics
P. 4296. At what speed must a pebble be thrown at a height of h, and at an angle of 30o, measured from the horizontal, if it is to hit the ground at an angle of 45o. (Air drag can be neglected.)
(4 pont)
solution (in Hungarian), statistics
P. 4297. A double cone which ``rolls up'' on a slope is a well known playful experiment. The slope is made of two lathes. The angle between the inclined plane determined by the two lathes and the horizontal is  , and the angle between the steepest line along the inclined plane and a lath is
, and the angle between the steepest line along the inclined plane and a lath is  . What is the half vertex angle
. What is the half vertex angle 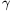 of that double cone which can roll up on this slope?
of that double cone which can roll up on this slope?
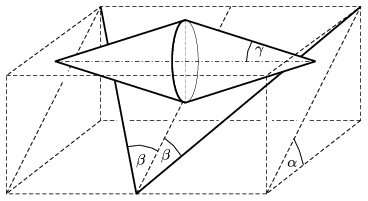
(5 pont)
solution (in Hungarian), statistics
P. 4298. A carpet runner is placed onto a long straight inclined plane parallel to the steepest line in the plane, from the bottom of the slope till its top. The carpet is thin and flexible, and it cannot slide down because of the friction, but it can easily be lifted, it does not stick to the plane. The top end of the carpet is rolled, a bit, and this hoop of carpet is released. The hoop rolls down the slope with greater and greater speed, while its diameter increases, and finally it reaches the bottom of the slope during a time of t1. If a solid cylinder is released at the top of the slope, it reaches the bottom in a time of t2. a) Which motion lasts longer the motion of the carpet or the motion of the cylinder? b) Calculate the ratio of t1/t2.
(6 pont)
solution (in Hungarian), statistics
P. 4299. A thin, solid uniform rod of length L is placed into a right-angled corner of a wall, and its point A at the bottom of the rod is moved at a uniform velocity of vA, such that the rod always remains in the plane which is perpendicular to the wall and the floor. How far will the bottom end of the initially vertical rod be from the wall, when the top end is disconnected from the wall? (Data: vA=3.5 m/s, L=2 m.)
(5 pont)
solution (in Hungarian), statistics
P. 4300. After leaving the runway a supersonic fighter begins to ascend along a straight line of angle of elevation of 30o. Due to the the abrupt sound wave the grass in the fields around the runway spread out in a parabolic shape. What is the speed of the fighter?
(5 pont)
solution (in Hungarian), statistics
P. 4301. The radius of a thin ring of mass M floating in space is R.
a) At which point of the straight line which goes through the centre of the ring and which is perpendicular to the plane of the ring will the force exerted on a small pointlike object be the greatest? (Where will the gravitational field strength be the greatest?)
b) If a pointlike object of mass m (m M) is released at such a point, what is its relative speed at which it crosses the ring?
M) is released at such a point, what is its relative speed at which it crosses the ring?
(5 pont)
solution (in Hungarian), statistics
P. 4302. There is some Oxygen gas in a vertical, long enough, metal, cylinder, above a piston of mass m=60 kg, and of cross section A=2 dm2. The cylinder is closed at its top and the piston hangs on a thread of length  0=11.2 dm. The initial pressure and temperature of the gas are equal to the pressure and temperature outside the cylinder, p0=105 Pa T0=273 K, respectively. The wall of the cylinder is a good heat conductor, and the piston can move in the cylinder without friction. By what amount will the total energy of the system change if the thread breaks?
0=11.2 dm. The initial pressure and temperature of the gas are equal to the pressure and temperature outside the cylinder, p0=105 Pa T0=273 K, respectively. The wall of the cylinder is a good heat conductor, and the piston can move in the cylinder without friction. By what amount will the total energy of the system change if the thread breaks?
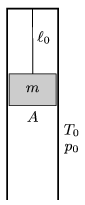
(4 pont)
solution (in Hungarian), statistics
P. 4303. What is the resistance of the resistor R shown in the figure if a) there is no current in the branch AB; b) the current in AC is the greatest; c) the potential difference between points a and C is maximum; d) the power at R is maximum; e) the current in branch DC is maximum; f) the current in AB is the maximum? (Data: U1=60 V, U2=20 V, R1=80 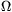 , R2=320
, R2=320 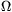 .)
.)
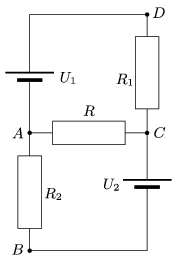
(4 pont)
solution (in Hungarian), statistics
P. 4304. There are more spectral lines in the emission spectrum of glowing gases, than in the absorption spectrum of cold gases. So there might be several lines which can be found in the emission spectrum, and which cannot be seen in the absorption spectrum of cold gases. Why?
(4 pont)
Upload your solutions above.
